Question

20、如图，在黄金水道长江上有A、B两艘运砂船在航行．A船测得航标灯C在北偏东52°方向上，测得船B在北偏东82°方向上．而此时B船测得航标灯C在北偏西36°的方向上．现在你能帮B船算出它对于A，C的视角∠ABC的大小吗．

Answer 1

分析：根据方向角的知识得出∠EAC=52°，∠EAD=82°，∠FBC=36°，从而可得∠ACD=52°，∠CAB=30°，根据∠ACB=∠ACD+∠BCD可得出∠ACB的度数，再由△ABC的内角和定理可得出∠ABC的大小．

解答：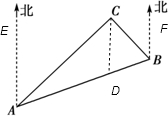
解：由题意得：∠EAC=52°，∠EAD=82°，∠FBC=36°，
∴∠ACD=∠EAC=52°，∠BCD=∠FBC=36°，
∴∠ACB=∠ACD+∠BCD=88°，
在△ABC中，∠ABC=180°-∠CAB-∠ABC=62°．

点评：本题考查方向角的知识，难度一般，关键是理解方向角的定义及在图形中所表示的角，另外解答本体还要运用三角形的内角和为180°这一知识点．