题目内容
一次函数y=-| k+1 |
| k |
| 2 |
| k |
分析:首先求出一次函数y=-
x+
(k为正整数)与x轴、y轴的交点坐标A、B两点,然后表示出Rt△AOB的面积Sk,再用拆项法
表示出Sk,进而求出S1+S2+S3+…+S2005的值.
| k+1 |
| k |
| 2 |
| k |
表示出Sk,进而求出S1+S2+S3+…+S2005的值.
解答:解:∵一次函数y=-
x+
(k为正整数)与x轴、y轴分别交于A、B两点,
∴当y=0,可求得:A(
,0),
当x=0,可求得:B(0,
),
∴Sk=
=2(
-
),
所以S1+S2+S3+…+S2005=2[(1-
)+(
-
)+(
-
)+…+(
-
)],
=2(1-
),
=
.
| k+1 |
| k |
| 2 |
| k |
∴当y=0,可求得:A(
| 2 |
| k+1 |
当x=0,可求得:B(0,
| 2 |
| k |
∴Sk=
| 2 |
| k(k+1) |
| 1 |
| k |
| 1 |
| k+1 |
所以S1+S2+S3+…+S2005=2[(1-
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 3 |
| 1 |
| 3 |
| 1 |
| 4 |
| 1 |
| 2005 |
| 1 |
| 2006 |
=2(1-
| 1 |
| 2006 |
=
| 2005 |
| 1003 |
点评:此题主要考查了一次函数与坐标轴的交点求法,以及与坐标轴围成的面积求法等知识,将Sk=
=2(
-
)进行拆项,是解决问题的关键.
| 2 |
| k(k+1) |
| 1 |
| k |
| 1 |
| k+1 |

练习册系列答案
 期末100分闯关海淀考王系列答案
期末100分闯关海淀考王系列答案 小学能力测试卷系列答案
小学能力测试卷系列答案
相关题目
为保护学生视力,课桌椅的高度都是按一定的关系配套设计的,研究表明:假设课桌的高度为ycm,椅子的高度为xcm,则y应是x的一次函数,下表列出两套符合条件的课桌椅的高度:第一套第二套椅子高度xcm桌子高度ycm.
(1)请确定y与x的函数关系式.
(2)现有一把高39cm的椅子和一张高为78.2的课桌,它们是否配套?为什么?
| 第一套 | 第二套 | |
| 椅子高度xcm | 40 | 37 |
| 桌子高度ycm | 75 | 70 |
(2)现有一把高39cm的椅子和一张高为78.2的课桌,它们是否配套?为什么?
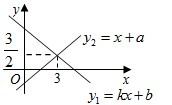 一次函数y1=kx+b与y2=x+a的图象如图,下列结论中:
一次函数y1=kx+b与y2=x+a的图象如图,下列结论中: