Question

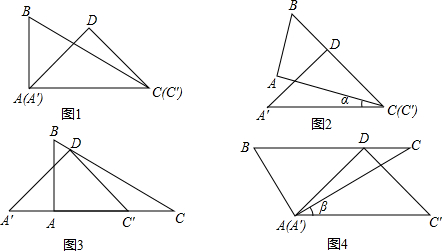
一副直角三角板由一块含30°的直角三角板与一块等腰直角三角板组成，且含30°角的三角板的较长直角边与另一三角板的斜边相等（如图1）

（1）如图1，这副三角板中，已知AB=2，AC=______

Answer 1

【答案】分析：（1）根据直角三角形中30°的直角边所对的直角边等于斜边的一半，即可求得BC的长，然后根据勾股定理即可求得AC的长；
（2）①根据三角板的度数即可求解；
②作DH⊥A′C于H，易证△CDH∽△CBA，根据相似三角形的对应边的比相等，即可求得CH的长，进而求得CC′；
③作DH⊥A′C′于H，AG⊥BC于G，可以证得Rt△AGD≌Rt△DHA，则BC∥AC′，利用平行线的性质即可求解；
（3）分0＜x＜3-，3-＜x≤，＜x≤2，x＞2四种情况即可求解．
解答：解：（1）∵直角△ABC中，∠BAC=30°，
∴BC=2AB=4．
∴AC==2．
在等腰直角直角△A′DC′中，A′C′=2，
∴A′D=A′C′=．

（2）①α=45°-30°=15°；
②作DH⊥A′C于H，则DH=A′C′=C′H=．
∵DH∥AB，
∴△CDH∽△CBA．
∴=，即=，
∴CH=3．
∴CC′=CH-C′H=3-，即m=CC′=3-；
③作DH⊥A′C′于H，AG⊥BC于G．
由已知：DH=，
AG×BC=AB×AC，
∴AG===，
∴AG=DH．
在Rt△AGD和Rt△DHA中：，
∴Rt△AGD≌Rt△DHA．
∴∠GDA=∠DAH=45°，
∴BC∥AC′，
∴β=∠OHA=30°；

（3）y=，
点评：本题考查了旋转的性质：旋转前后两图形全等，即对应相等相等，对应角相等；对应点与旋转中心的连线段的夹角等于旋转角．也考查了含30°的直角三角形三边的关系以及等腰直角三角形的性质．