题目内容
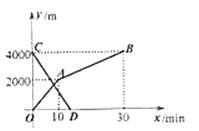
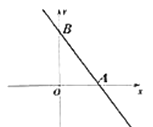
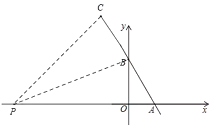
【题目】如图,一次函数![]() 的图像与
的图像与![]() 轴、
轴、![]() 轴交于
轴交于![]() 、
、![]() 两点,
两点,![]() 是
是![]() 轴正半轴上的一个动点,连接
轴正半轴上的一个动点,连接![]() ,将
,将![]() 沿
沿![]() 翻折,点
翻折,点![]() 恰好落在
恰好落在![]() 上,则点
上,则点![]() 的坐标为______.
的坐标为______.
【答案】(![]() ,0)或(24,0)
,0)或(24,0)
【解析】
分两种情况讨论:当点P在OA上时,由O与C关于PB对称,可得OP=CP,BC=OB=8;当点P在AO延长线上时,由O与C关于PB对称,可得OP=CP,BC=OB=8,分别依据勾股定理得到方程,解方程即可得到点P的坐标.
解:设点O关于直线PB的对称点是C.
∵一次函数![]() 的图象与x轴、y轴交于A、B两点,
的图象与x轴、y轴交于A、B两点,
∴AO=6,BO=8,AB=10.
分两种情况:
①当点P在OA上时,
由折叠的性质,可得OP=CP,BC=OB=8,∠BCP=∠BOP=90°.
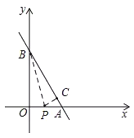
设OP=CP=x,则AP=6x,AC=108=2,
在Rt△ACP中,由勾股定理可得:x2+22=(6x)2,
解得x=![]() ,
,
∴P(![]() ,0);
,0);
②当点P在AO延长线上时,
由折叠的性质,可得OP=CP,BC=OB=8,∠C=∠BOP=90°.
设OP=CP=x,则AP=6+x,AC=10+8=18,
在Rt△ACP中,由勾股定理可得:x2+182=(6+x)2,
解得x=24,
∴P(24,0).
故答案为:(![]() ,0)或(24,0).
,0)或(24,0).

练习册系列答案
 轻松暑假总复习系列答案
轻松暑假总复习系列答案
相关题目