题目内容
已知实数a、b、c、d互不相等,且a+| 1 |
| b |
| 1 |
| c |
| 1 |
| d |
| 1 |
| a |
分析:由已知a+
=x; b+
=x;c+
=x;d+
=x;得出a与b的关系式,进而得出a与c的关系式,得出a与d的关系式,分析得出x的值.
| 1 |
| b |
| 1 |
| c |
| 1 |
| d |
| 1 |
| a |
解答:解:由已知有a+
=x,①; b+
=x,②;c+
=x,③;d+
=x,④;
由①解出b=
⑤代入②得c=
⑥
将⑥代入③得
+
=x
即dx3-(ad+1)x2-(2d-a)x+ad+1=0⑦
由④得ad+1=ax,代入⑦得(d-a)(x3-2x)=0
由已知d-a≠0,∴x3-2x=0
若x=0,则由⑥可得a=c,矛盾.
故有x2=2,x=±
| 1 |
| b |
| 1 |
| c |
| 1 |
| d |
| 1 |
| a |
由①解出b=
| 1 |
| x-a |
| x-a |
| x2-ax-1 |
将⑥代入③得
| x-a |
| x2-ax-1 |
| 1 |
| d |
即dx3-(ad+1)x2-(2d-a)x+ad+1=0⑦
由④得ad+1=ax,代入⑦得(d-a)(x3-2x)=0
由已知d-a≠0,∴x3-2x=0
若x=0,则由⑥可得a=c,矛盾.
故有x2=2,x=±
| 2 |
点评:此题主要考查了分式的等式变形,运用未知数简介代换得出两式相乘等于0的形式,是解决问题的关键.

练习册系列答案
 53随堂测系列答案
53随堂测系列答案
相关题目
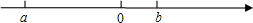 已知实数a、b在数轴上的位置如图.
已知实数a、b在数轴上的位置如图.