��Ŀ����
����Ŀ��������ѧ��֯ѧ����չ���ʵ���������ij�������������֪ʶ���˽�̶ȣ�A���ر���Ϥ��B�������˽⣬C����֪�������ڸ����������ȡ��100����������ʾ����飬���������Ƴ���ͼ��ʾ��ͳ��ͼ������ͳ��ͼ����������⣺
��1�����������о���900�ˣ��Թ��ƶ�����֪ʶ���ر���Ϥ���ľ���������
��2���������Ĺ�����Ա���С�Ů��2����������ѡ2���μ�����֪ʶ��ѵ�������б�����״ͼ�ķ�������ǡ��ѡ��һ��һŮ�ĸ��ʣ�
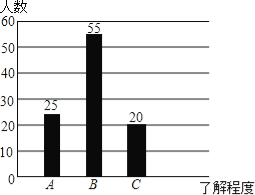
���𰸡���1��������֪ʶ���ر���Ϥ���ľ�������Ϊ225
��2��ǡ��ѡ��һ��һŮ�ĸ���Ϊ![]() ��
��
��������
���⣨1������������ж�����֪ʶ���ر���Ϥ���ľ�����ռ�İٷֱȣ�Ȼ���ٳ����������ɣ�
��2����A1��A2��ʾ�������Թ�����Ա��B1��B2��ʾ����Ů�Թ�����Ա���г��������״ͼ���ٸ��ݸ��ʹ�ʽ��⣮
�����������1���ڵ���ľ����У�������֪ʶ���ر���Ϥ���ľ�����ռ�İٷֱ�Ϊ��![]() ��100%=25%��
��100%=25%��
������������֪ʶ���ر���Ϥ���ľ�����������Ϊ900��25%=225��
��2����A1��A2��ʾ�������Թ�����Ա��B1��B2��ʾ����Ů�Թ�����Ա���б�����״ͼ���£�

��ǡ��ѡ��һ��һŮ�ĸ���Ϊ��![]() ��
��

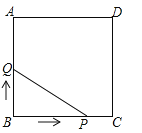
 ��ĩ100�ִ��غ�������ϵ�д�
��ĩ100�ִ��غ�������ϵ�д� Сѧ�������Ծ�ϵ�д�
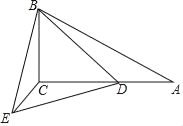
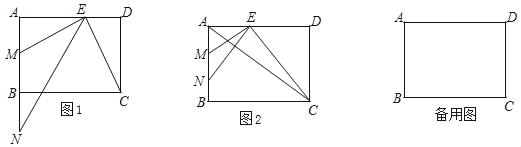
Сѧ�������Ծ�ϵ�д�����Ŀ����ͼ����P�ǻ�AB������AB��һ���㣬����P��PC��AB��AB�ڵ�P��������AC����AB�ڵ�D����֪AB��6cm��PC��1cm����A��P�����ľ���Ϊxcm��A��D�����ľ���Ϊycm��������P���A�غ�ʱ��y��ֵΪ0��
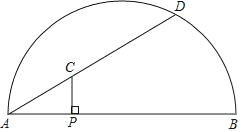
Сƽ����ѧϰ�����ľ��飬�ֱ�Ժ���y���Ա���x�ı仯���仯�Ĺ��ɽ�����̽����
������Сƽ��̽�����̣��벹��������
��1�������±����Ա���x��ֵ����ȡ�㡢��ͼ���������ֱ�õ���y��x�ļ����Ӧֵ��
x/cm | 0 | 1 | 2 | 3 | 4 | 5 | 6 |
y1/cm | 0 | 4.24 | 5.37 | m | 5.82 | 5.88 | 5.92 |
������m��ֵ���� ��������һλС������
��2����ͬһƽ��ֱ������ϵxOy�У������ȫ��ı��и�����ֵ����Ӧ�ĵ㣨x��y��������������y��ͼ����

��3����Ϻ���ͼ������⣺����PAC��30�㣬AD�ij���ԼΪ�� ��cm��