��Ŀ����
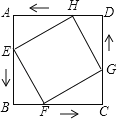
����Ŀ����ͼ����һ�鳤Ϊ50cm����Ϊ30cm�ij�������Ƭ����һ���ǵĺ��ӣ�������Ƭ���ĸ��ǽ�ȥ�ĸ���ͬ��С�����Σ���С�����εı߳�Ϊxcm��

��1������ij�AB���� cm����BC���� cm���ú�x�Ĵ���ʽ��ʾ��
��2�������ɺ��ӵĵ����Ϊ300cm2ʱ����ú��ӵ��ݻ���
��3���ú��ӵIJ����S�Ƿ������������������ڣ����x��ֵ�����ֵ�Ƕ��٣��������ڣ�˵�����ɣ�
���𰸡���1��50��2x��30��2x����2����x1��10ʱ�������ݻ�Ϊ3000cm3����3����x��10ʱ��S�����ֵ�����ֵΪ800��
��������
��1�����ó����εij�����Լ�����Ƭ���ĸ��ǽ�ȥ�ĸ���ͬ��С�����Σ��ó�AB��BC�ij����ɣ�
��2�����ã�1���г�����Լ����ӵĵ����Ϊ300cm2ʱ�ó�x��ֵ�����ɵ�������ӵ��ݻ���
��3�����ú��Ӳ����Ϊ��S=2x��50-2x��+2x��30-2x�����������䷽�������ֵ���ɣ�
��1������һ�鳤Ϊ50cm����Ϊ30cm�ij�������Ƭ����һ���ǵĺ��ӣ�����Ƭ���ĸ��ǽ�ȥ�ĸ���ͬ��С�����Σ�
��С�����εı߳�Ϊxcm��
������ij�AB����50��2x��cm����BC����30��2x��cm��
�ʴ�Ϊ��50��2x��30��2x��
��2�������⣬�ã�
��50��2x����30��2x����300
�������ã�x2��40x+300��0
��ã�x1��10��x2��30�����������⣬��ȥ��
��x1��10ʱ�������ݻ�����50��20����30��20����10��3000��cm3����
��3�����ӵIJ����Ϊ��
S��2x��50��2x��+2x��30��2x��
��100x��4x2+60x��4x2
����8x2+160x����8��x2��20x��
����8[��x��10��2��100]
����8��x��10��2+800
����8��x��10��2��0��
����8��x��10��2+800��800��
����x��10ʱ��S�����ֵ�����ֵΪ800��

 һŵ��ҵ�����ҵ���ּ�����������������ϵ�д�
һŵ��ҵ�����ҵ���ּ�����������������ϵ�д�