题目内容
在2ABCD中，对角线BD、AC相交于点O，BE=DF，过点O作线段GH交AD于点G，交BC于点H，顺次连接EH、HF、FG、GE，求证：四边形EHFG是平行四边形。
在2ABCD中
AD//BC，AO=CO，BO=DO
∴
GAO=HCO
在
AGO和CHO中
GAO=HCO
AO=CO
GOA=HOC
∴AGO≌CHO
∴GO=HO
又∵BO=DO，BE=DF
∴EO=FO
∴四边形EHFG为平行四边形。
AD//BC，AO=CO，BO=DO
∴
GAO=HCO在
AGO和CHO中GAO=HCOAO=CO
GOA=HOC∴
AGO≌CHO∴GO=HO
又∵BO=DO，BE=DF
∴EO=FO
∴四边形EHFG为平行四边形。
要证四边形EHFG是平行四边形，需证OG=OH，OE=OF，可分别由四边形ABCD是平行四边形和△OAG≌△OCH得出．
练习册系列答案
相关题目
的图像交点为A，B。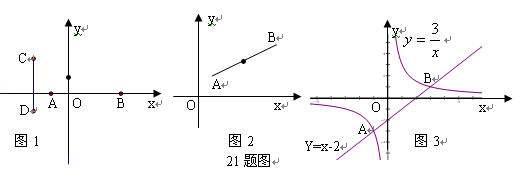
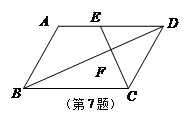
中，
、
分别是
、
的中点，若
，则菱形
②CE=CF ③∠AEB=750 ④BE+DF=EF ⑤
其中正确的是 （只填写序号）