题目内容
已知(x-y+2)的算术平方根和(x+y-1)2互为相反数,则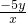 的平方根为________.
的平方根为________.
±
分析:先根据互为相反数的和等于0列式,再根据非负数的性质列式求出x、y的值,然后代入代数式进行计算,最后根据平方根的定义进行求解.
解答:∵(x-y+2)的算术平方根和(x+y-1)2互为相反数,
∴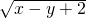 +(x+y-1)2=0,
+(x+y-1)2=0,
∴x-y+2=0,x+y-1=0,
解得x=- ,y=
,y= ,
,
∴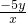 =
=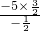 =15,
=15,
∴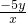 的平方根为±
的平方根为± .
.
故答案为:± .
.
点评:本题考查了算术平方根非负数,平方数非负数的性质,以及平方根的定义,根据几个非负数的和等于0,则每一个算式都等于0列式是解题的关键.

分析:先根据互为相反数的和等于0列式,再根据非负数的性质列式求出x、y的值,然后代入代数式进行计算,最后根据平方根的定义进行求解.
解答:∵(x-y+2)的算术平方根和(x+y-1)2互为相反数,
∴
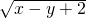 +(x+y-1)2=0,
+(x+y-1)2=0,∴x-y+2=0,x+y-1=0,
解得x=-
 ,y=
,y= ,
,∴
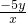 =
=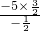 =15,
=15,∴
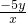 的平方根为±
的平方根为± .
.故答案为:±
 .
.点评:本题考查了算术平方根非负数,平方数非负数的性质,以及平方根的定义,根据几个非负数的和等于0,则每一个算式都等于0列式是解题的关键.

练习册系列答案
相关题目

 E作
E作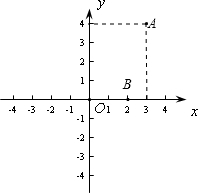 已知函数y=x2+bx+c的图象经过A(3,4)和B(2,0)两点.
已知函数y=x2+bx+c的图象经过A(3,4)和B(2,0)两点.