题目内容
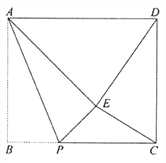
【题目】如图,在矩形![]() 纸片中,
纸片中,![]() cm,
cm,![]() cm。点
cm。点![]() 在
在![]() 边上,将
边上,将![]() 沿
沿![]() 折叠,得
折叠,得![]() ,连接
,连接![]() ,
, ![]() .
.
(1)当点![]() 落在
落在![]() 边上时,
边上时,![]() ;
;
(2)当点![]() 是
是![]() 的中点时,求
的中点时,求![]() 的长;
的长;
(3)当![]() 分别满足下列条件时,求相应的
分别满足下列条件时,求相应的![]() 的长:
的长:
①![]() ;②
;②![]() .
.
【答案】(1)2![]() ; (2)
; (2)![]() ;(3)①
;(3)①![]() ;②
;②![]() .
.
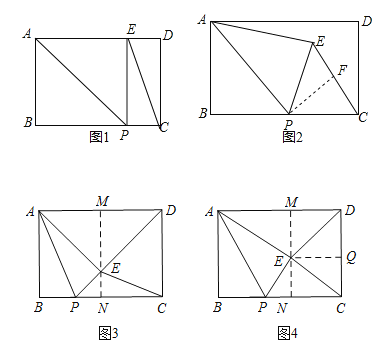
【解析】(1)如图1,根据已知条件得到四边形ABPE是正方形,求得PC=2,根据勾股定理得到CE的长;
(2)如图2,取CE的中点F,连接PF,由点P是BC的中点,得到PB=PC=6,根据勾股定理得到PA的长,根据折叠的性质得到∠APE=∠APB,PE=PB=6, PC=PE,根据等腰三角形的性质得到∠EPF=∠CPF,∠PFC=90°,CE=2CF,由余角的性质得到∠CPF=∠PAB,根据相似三角形的得到CF的长,于是得到结论;
(3)①如图3,过E作MN⊥AD于M,交BC于N,则MN⊥BC,根据勾股定理得到ME的长,求得EN=MN﹣ME=2,根据相似三角形的性质得到PB的长;
②如图3,过E作EQ⊥CD于Q,根据勾股定理和相似三角形的性质即可得到结论.
(1)如图1.∵将△PAB沿AP折叠,得△PAE,∴四边形ABPE是正方形,
∴PB=PE=AB=10,∴PC=2,∴CE=![]() =2
=2![]() .
.
故答案为:2![]() ;
;
(2)如图2,取CE的中点F,连接PF.
∵点P是BC的中点,∴PB=PC=6.
∵AB=10,∴PA=![]() =2
=2![]() .
.
∵将△PAB沿AP折叠,得△PAE,∴∠APE=∠APB,PE=PB=6,∴PC=PE.
∵点F是CE的中点,∴∠EPF=∠CPF,∠PFC=90°,CE=2CF,∴∠APF=90°,∴∠APB+∠CPF=∠APB+∠PAB=90°,∴∠CPF=∠PAB,∴△PAB∽△CPF,∴![]() ,∴CF=
,∴CF=![]() ,∴CE=2CF=
,∴CE=2CF=![]() ;
;
(3)①如图3,过E作MN⊥AD于M,交BC于N,则MN⊥BC.
∵DE=CD,AE=AB=CD=DE,∴AE=10,∴AM=![]() AD=6=BN,∴ME=
AD=6=BN,∴ME=![]() =8,∴EN=MN﹣ME=2,易知,△AME∽△ENP,∴
=8,∴EN=MN﹣ME=2,易知,△AME∽△ENP,∴![]() ,∴PE=PB=
,∴PE=PB=![]() ,∴PB=
,∴PB=![]() ;
;
②如图4,过E作EQ⊥CD于Q.∵DE=CE,∴DQ=![]() CD=5,∴ME=5,∴EN=MN﹣ME=5,∴AM=
CD=5,∴ME=5,∴EN=MN﹣ME=5,∴AM=![]() =5
=5![]() ,∴BN=5
,∴BN=5![]() ,同理得:
,同理得:![]() ,∴PE=PB=
,∴PE=PB=![]() ,∴PB=
,∴PB=![]() .
.