题目内容
(1)计算: ;
;
(2)先化简,再求值: ,其中,a是方程x2+3x+1=0的根.
,其中,a是方程x2+3x+1=0的根.
解:(1)原式=-9+1-4×,
= +2,
+2,
=-8;(4分)
(2)原式=[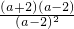 +
+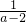 ]×
]× (2分)
(2分)
=( +
+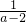 )×
)×
=
= (a2+3a),(4分)
(a2+3a),(4分)
∵a是方程x2+3x+1=0的根,
∴a2+3a+1=0,
∴a2+3a=-1,(5分)
∴原式= .(6分)
.(6分)
故答案为:-8,- .
.
分析:(1)分别根据零指数幂、乘方、特殊角的三角函数值、负整数指数幂的运算法则进行计算,然后根据实数的运算法则求得计算结果;
(2)先把已知代数式进行化简,再根据a是方程x2+3x+1=0的根求出a的值,代入所求代数式进行计算即可.
点评:本题考查的是实数的综合运算能力及代数求值,熟记特殊角的三角函数值,熟练掌握负整数指数幂、零指数幂等考点的运算是解答此类题目的关键.
=
 +2,
+2,=-8;(4分)
(2)原式=[
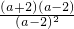 +
+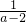 ]×
]× (2分)
(2分)=(
 +
+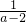 )×
)×
=

=
 (a2+3a),(4分)
(a2+3a),(4分)∵a是方程x2+3x+1=0的根,
∴a2+3a+1=0,
∴a2+3a=-1,(5分)
∴原式=
 .(6分)
.(6分)故答案为:-8,-
 .
.分析:(1)分别根据零指数幂、乘方、特殊角的三角函数值、负整数指数幂的运算法则进行计算,然后根据实数的运算法则求得计算结果;
(2)先把已知代数式进行化简,再根据a是方程x2+3x+1=0的根求出a的值,代入所求代数式进行计算即可.
点评:本题考查的是实数的综合运算能力及代数求值,熟记特殊角的三角函数值,熟练掌握负整数指数幂、零指数幂等考点的运算是解答此类题目的关键.

练习册系列答案
 亮点激活精编提优100分大试卷系列答案
亮点激活精编提优100分大试卷系列答案
相关题目
