题目内容
已知矩形ABCD中,BE平分∠ABC交矩形的一条边于点E,若BD=10,∠EBD=15°,则AB= .
【答案】分析:化成符合条件的两种情况,根据矩形性质求出∠A=∠ABC=∠C=90°,∠ABE=∠CBE=45°,求出∠DBC和∠ABD的度数,求出CD和AD,即可求出AB.
解答:解:有两种情况:如图

∵四边形ABCD是矩形,
∴∠A=∠ABC=∠C=90°,
∵BE平分∠ABC,
∴∠ABE=∠CBE=45°,
图1中,∵∠EBD=15°,
∴∠DBC=30°,
∴CD= BD=5,
BD=5,
即AB=CD=5;
图2中,∵∠EBD=15°,
∴∠ABD=30°,
∴AD= BD=5,
BD=5,
在Rt△ABD中,由勾股定理得:AB= =5
=5 .
.
故答案为:5或5 .
.
点评:本题考查了矩形性质和含30度角的直角三角形性质,勾股定理的应用,关键是化成符合条件的所有情况,题目比较典型,是一道比较好的题目.
解答:解:有两种情况:如图

∵四边形ABCD是矩形,
∴∠A=∠ABC=∠C=90°,
∵BE平分∠ABC,
∴∠ABE=∠CBE=45°,
图1中,∵∠EBD=15°,
∴∠DBC=30°,
∴CD=
 BD=5,
BD=5,即AB=CD=5;
图2中,∵∠EBD=15°,
∴∠ABD=30°,
∴AD=
 BD=5,
BD=5,在Rt△ABD中,由勾股定理得:AB=
 =5
=5 .
.故答案为:5或5
 .
.点评:本题考查了矩形性质和含30度角的直角三角形性质,勾股定理的应用,关键是化成符合条件的所有情况,题目比较典型,是一道比较好的题目.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
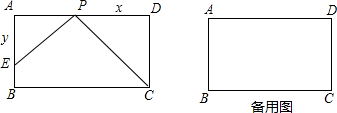
 ,点Q从点B以每秒1个单位沿BA方向向点A运动,设运动时间为t秒,△BPQ的面积为S.
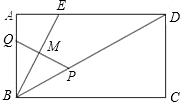
,点Q从点B以每秒1个单位沿BA方向向点A运动,设运动时间为t秒,△BPQ的面积为S. 如图,已知矩形ABCD中,BC=6,AB=8,延长AD到点E,使AE=15,连接BE交AC于点P.
如图,已知矩形ABCD中,BC=6,AB=8,延长AD到点E,使AE=15,连接BE交AC于点P. 如图:已知矩形ABCD中,CE∥DF.
如图:已知矩形ABCD中,CE∥DF.