题目内容
如图所示，己知⊙O的弦AB垂直于直径CD，垂足为F，点E在AB上，且EA=EC。
(1)求证：AC2=AE?AB
(2)延长EC到点P，连结PB，若PB=PE，试判断PB与⊙O的位置关系，并说明理由。
(1)证明：连结BC，因为AB⊥CD，CD为⊙O的直径，所以BC=AC，所以∠1=∠2，
又因为AE=CE,所以∠1=∠3，所以△AEC∽△ACB，所以
，
即AC2=AB?AE。
(2)PB与⊙O相切，理由：连结OB，因为PB=PE，所以∠PBE=∠PEB，
因为∠l=∠2=∠3，所以∠PEB=∠1+∠3=2∠1，而∠PBE=∠2+∠PBC，
所以∠OBC=∠OCB，而Rt△BCF中，∠OCB=90°一∠2=90°一∠1，
所以∠OBC=90°一∠l，所以∠OBP=∠OBC+∠PBC=∠1+(90°一∠1)=90°，
所以PB⊥OB，即PB为⊙O的切线。(证明方法不唯一)
练习册系列答案
相关题目
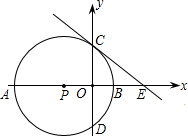D，其中A（-3，0），B（1，0）．过点C作⊙P的切线交x轴于点E．
如图所示，己知AD与AB，CD交于A，D两点，EC，BF与AB，CD交于点E，C，B，F，且∠1=∠2，∠B=∠C．
如图所示，己知△ABC．