Question

在平面直角坐标系中，已知A（0，3），B（4，0），设P、Q分别是线段AB、OB上的动点，它们同时出发，点P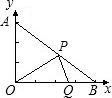以每秒3个单位的速度从点A向点B运动，点Q以每秒1个单位的速度从点B向点O运动．设运动时间为t（秒）．
（1）用含t的代数式表示点P的坐标；
（2）当t为何值时，△OPQ为直角三角形？
（3）在什么条件下，以Rt△OPQ的三个顶点能确定一条对称轴平行于y轴的抛物线？选择一种情况，求出所确定的抛物线的解析式．

Answer 1

分析：（1）作PM⊥y轴，PN⊥x轴，那么PM就是P点的横坐标，PN就是P点的纵坐标．然后可通过相似三角形AMP和AOB求出MP的长，同理可通过相似三角形BPN和BAP求出PN的长，即可得出P点的坐标．
（2）本题要分情况进行讨论：
①当∠POQ=90°时，P，A重合此时t=0；
当∠OPQ=90°时，可根据射影定理得出PN²=ON•NQ，由此可求出t的值．
当∠OPQ=90°时，Q，N重合，可用BQ的长表示出P点的横坐标，以此可求出t的值．
（3）很显然当∠OPQ=90°时，可确定一条符合条件的抛物线，可根据（2）中得出的∠OPQ=90°时t的取值，确定出P，Q的坐标，然后用待定系数法即可求出这条抛物线的解析式．

解答：解：（1）作PM⊥y轴，PN⊥x轴．
∵OA=3，OB=4，
∴AB=5．
∵PM∥x轴，
∴

PM

OB

=

AP

AB

，
∴

PM

4

=

3t

5

，
∴PM=

12

5

t．
∵PN∥y轴，
∴

PN

OA

=

PB

AB

，
∴

PN

3

=

5-3t

5

，
∴PN=3-

9

5

t，
∴点P的坐标为（

12

5

t，3-

9

5

t）．

（2）①当∠POQ=90°时，t=0，△OPQ就是△OAB，为直角三角形．
②当∠OPQ=90°时，△OPN∽△PQN，
∴PN²=ON•NQ．
（3-

9

5

t）²=

12

5

t（4-t-

12

5

t）．
化简，得19t²-34t+15=0，
解得t=1或t=

15

19

．
③当∠OQP=90°时，N、Q重合．
∴4-t=

12

5

t，
∴t=

20

17

．
综上所述，当t=0，t=1，t=

15

19

，t=

20

17

时，△OPQ为直角三角形．

（3）当t=1或t=

15

19

时，即∠OPQ=90°时，
以Rt△OPQ的三个顶点可以确定一条对称轴平行于y轴的抛物线．
当t=1时，点P、Q、O三点的坐标分别为P（

12

5

，

6

5

），Q（3，0），O（0，0）．
设抛物线的解析式为y=a（x-3）（x-0），
即y=a（x²-3x）．
将P（

12

5

，

6

5

）代入上式，
得a=-

5

6

．
∴y=-

5

6

（x²-3x）．
即y=-

5

6

x²+

5

2

x．
说明：若选择t=

15

19

时，点P、Q、O三点的坐标分别是P（

36

19

，

30

19

），Q（

61

19

，0），O（0，0）．
求得抛物线的解析式为y=-

19

30

x²+

61

30

x．

点评：本题着重考查了待定系数法求二次函数解析式、三角形相似、直角三角形的判定等知识点，考查学生分类讨论，数形结合的数学思想方法．