题目内容

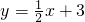已知：一次函数 $数学公式$ 的图象与正比例函数y=kx的图象相交于点A（a，1）．
（1）求a的值及正比例函数y=kx的解析式；
（2）点P在坐标轴上（不与点O重合），若PA=OA，直接写出P点的坐标；
（3）直线x=m与一次函数的图象交于点B，与正比例函数图象交于点C，若△ABC的面积记为S，求S关于m的函数关系式（写出自变量的取值范围）．

解：（1）∵一次函数y= $\text{[math]}$ x+3的图象与正比例函数y=kx的图象相交于点
A（a，1），
∴ $\text{[math]}$ a+3=1．
解得a=-4．
∴A（-4，1）．
∴-4k=1．
解得k=- $\text{[math]}$ ．
∴正比例函数的解析式为y=- $\text{[math]}$ x；

（2）如图1，P₁（-8，0）或P₂（0，2）；

（3）依题意，得点B的坐标为（m， $\text{[math]}$ m+3），点C的坐标为（m，- $\text{[math]}$ m）．
作AH⊥BC于点H，H的坐标为（m，1）．
以下分两种情况：
（ⅰ）当m＜-4时，
BC=- $\text{[math]}$ m-（ $\text{[math]}$ m+3）
=- $\text{[math]}$ m-3．
AH=-4-m．
则S_△ABC= $\text{[math]}$ BC•AH
= $\text{[math]}$ （- $\text{[math]}$ m-3）（-4-m）

= $\text{[math]}$ m²+3m+6；
（ⅱ）当m＞-4时，
BC=（ $\text{[math]}$ m+3）+ $\text{[math]}$ m= $\text{[math]}$ m+3．
AH=m+4．
则S_△ABC= $\text{[math]}$ BC•AH
= $\text{[math]}$ （ $\text{[math]}$ m+3）（4+m）
= $\text{[math]}$ m²+3m+6；
综上所述，S_△ABC= $\text{[math]}$ m²+3m+6（m≠-4）．
分析：（1）将A（a，1）代入一次函数y= $\text{[math]}$ x+3求出a的值，再将A点坐标代入正比例函数解析式求出k的值，从而得到正比例函数解析式；
（2）分两种情况：P在x轴上和P在y轴上，令PA=OA即可解答．
（3）依题意，得点B的坐标为（m， $\text{[math]}$ m+3），点C的坐标为（m，- $\text{[math]}$ m），作AH⊥BC于点H，H的坐标为（m，1）．然后分两种情况讨论：（ⅰ）当m＜-4时，（ⅱ）当m＞-4时．两种情况下，分别求出BC、AH的表达式，代入计算即可．
点评：本题考查了一次函数综合题，涉及函数图象与坐标轴的交点、三角形的面积与坐标之间的关系、同时考查了分类讨论与数形结合的数学思想．