Question

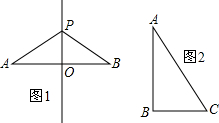
（1）如图1，已知△ABC，∠ACB=90°，AC=BC，点E、F在直线AB上，∠ECF=∠B，
①△ACF与△BEC的关系为______．
②设△ABC的面积为S，求证：AF•BE=2S．
（2）如图2，将（1）中的∠ACB=90°改为∠ACB=α°，求证：AF•BE=．
（3）如图3，在 （2）中的条件不变的情况下，（2）中的结论是否成立？（直接写出结论，不用说明理由）

Answer 1

【答案】分析：（1）①可证明∠A=∠B=45°，再根据外角的性质和已知条件可得出∠ACF=∠BEC，利用两对对应角相等的两个三角形相似可得出△ACF∽△BEC；
②利用相似三角形△ACF∽△BEC的对应边成比例、直角三角形的面积公式证得AF•BE=2S；
（2）利用两对对应角相等的两个三角形相似可得出△ACF∽△BEC；然后由相似三角形的对应边成比例、三角形的面积公式S=absinC证得结论；
（3）根据等边对等角证得∠A=∠CBA，再根据外角的性质和已知条件可得出∠AFC=∠BCE，利用两对对应角相等的两三角形相似可得出△ACF∽△BEC；然后由相似三角形的对应边成比例、三角形的面积公式S=absinC证得结论．
解答：（1）解：①△ACF∽△BEC，理由为：
∵∠ACB=90°，AC=BC，
∴∠A=∠B=45°，
∴∠BEC=∠ACE+∠A=∠ACE+45°，
∵∠ECF=45°，
∴∠ACF=∠ACE+45°，
∴∠ACF=∠BEC，又∠A=∠B，
∴△ACF∽△BEC．
故答案为：△ACF∽△BEC；

②证明：∵△ACF∽△BEC，
∴=，
∴AC•BC=BE•AF，
∴S_△ABC=AC•BC=BE•AF，
∴AF•BE=2S；

（2）证明：∵AC=BC，
∴∠A=∠CBA（等边对等角），
∴∠BEC=∠ACE+∠A（三角形外角定理）．
又∵∠ACF=∠ACE+∠ECF，∠ECF=∠CBA，
∴∠ACF=∠BEC，
又∵∠A=∠CBA，
∴△ACF∽△BEC；
∴=，
∴AC•BC=BE•AF，
∴S=AC•BCsin∠ACB=BE•AFsin∠ACB=BE•AFsinα，即AF•BE=．

（3）解：（2）中的结论能成立，理由如下：
∵AC=BC，
∴∠CAB=∠B（等边对等角），
∵∠AFC=∠B+∠FCB（三角形外角定理），∠BCE=∠ECF+∠FCB，∠ECF=∠B
∴∠AFC=∠BCE，又∠A=∠B，
∴△ACF∽△BEC；
∴=，
∴AC•BC=BE•AF，
∴S=AC•BCsin∠ACB=BE•AFsin∠ACB=BE•AFsinα，即AF•BE=．
点评：本题考查了相似综合题．涉及到的知识点有相似三角形的判定与性质、三角形外角定理、等腰三角形的性质以及三角形的面积公式．