题目内容
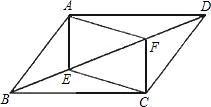
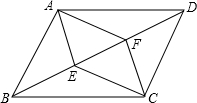 如图,E、F是平行四边形ABCD对角线BD上的两点,给出下列三个条件:
如图,E、F是平行四边形ABCD对角线BD上的两点,给出下列三个条件:
①BE=DF,②AF=CE,③∠AEB=∠CFD.
(1)请你从中选择一个适当的条件______(填序号),使四边形AECF是平行四边形,并加以证明;
(2)任选一个条件能使四边形AECF成为平行四边形的概率是______.
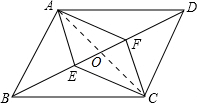 (1)选①作条件.
(1)选①作条件.证明:连接AC,
∵四边形ABCD是平行四边形,
∴AO=CO,BO=DO,
∵BE=DF,
∴BO-BE=DO-DF,
即EO=FO,
∴四边形AECF是平行四边形;
选③作条件.
证明:连接AC,
∵四边形ABCD是平行四边形,
∴AB∥CD,
∴∠CDF=∠ABE,AB=CD,
在△ABE和△CDF中
 ,
,∴△ABE≌△CDF(AAS),
∴BE=DF,
∵四边形ABCD是平行四边形,
∴AO=CO,BO=DO,
∵BE=DF,
∴BO-BE=DO-DF,
即EO=FO,
∴四边形AECF是平行四边形;
(2)解:共有3个条件,其中有两个可以使四边形AECF成为平行四边形,故概率为:
 ,
,故答案为:
 .
.分析:(1)选①作条件,连接AC,首先根据平行四边形的性质可得AO=CO,BO=DO,再加上条件BE=DF,可得EO=FO,进而可证出四边形AECF是平行四边形;
选③作条件,连接AC,首先证明△ABE≌△CDF可得BE=DF,再根据平行四边形的性质可得AO=CO,BO=DO,再加上条件BE=DF,可得EO=FO,进而可证出四边形AECF是平行四边形;
(2)根据概率公式:随机事件A的概率P(A)=事件A可能出现的结果数÷所有可能出现的结果数.
点评:此题主要考查了平行四边形的判定与性质,解决问题的关键是熟练掌握平行四边形的性质与判定方法.

练习册系列答案
 学练快车道快乐假期暑假作业新疆人民出版社系列答案
学练快车道快乐假期暑假作业新疆人民出版社系列答案 浙大优学小学年级衔接导与练浙江大学出版社系列答案
浙大优学小学年级衔接导与练浙江大学出版社系列答案 小学暑假作业东南大学出版社系列答案
小学暑假作业东南大学出版社系列答案
相关题目
 8、
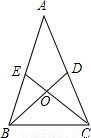
8、 1、如图,在△ABC中,D、E分别是AC、AB上的点,BD与CE交于点O,给出下列四个条件:①∠EBO=∠DCO;②∠BEO=∠CDO;③BE=CD;④OB=OC.
1、如图,在△ABC中,D、E分别是AC、AB上的点,BD与CE交于点O,给出下列四个条件:①∠EBO=∠DCO;②∠BEO=∠CDO;③BE=CD;④OB=OC.
 相交于点C.
相交于点C.
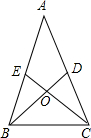 1、如图,在△ABC中,D、E分别是AC、AB上的点,BD与CE交于点O,给出下列四个条件:①∠EBO=∠DCO;②∠BEO=∠CDO;③BE=CD;④OB=OC.
1、如图,在△ABC中,D、E分别是AC、AB上的点,BD与CE交于点O,给出下列四个条件:①∠EBO=∠DCO;②∠BEO=∠CDO;③BE=CD;④OB=OC.