题目内容
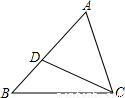
（2010•陕西）如图，A、B、C三点在同一条直线上，AB=2BC，分别以AB，BC为边做正方形ABEF和正方形BCMN连接FN，EC．求证：FN=EC．
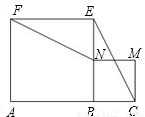
【答案】分析：只要判定△FNE≌△EBC，就不难证明FN=EC．
解答：证明：在正方形ABEF中和正方形BCMN中，
AB=BE=EF，BC=BN，∠FEN=∠EBC=90°，
∵AB=2BC，即BC=BN=
AB，
∴BN=
BE，即N为BE的中点，
∴EN=NB=BC，
∴△FNE≌△EBC，
∴FN=EC．
点评：本题集中考查了正方形的性质和全等三角形的判定．
（1）正方形的四条边相等，四个角相等，都是90°，对角线互相垂直、平分；
（2）三角形全等的判定定理有SAS、SSS、AAS，ASA，HL等．
解答：证明：在正方形ABEF中和正方形BCMN中，
AB=BE=EF，BC=BN，∠FEN=∠EBC=90°，
∵AB=2BC，即BC=BN=
AB，∴BN=
BE，即N为BE的中点，∴EN=NB=BC，
∴△FNE≌△EBC，
∴FN=EC．
点评：本题集中考查了正方形的性质和全等三角形的判定．
（1）正方形的四条边相等，四个角相等，都是90°，对角线互相垂直、平分；
（2）三角形全等的判定定理有SAS、SSS、AAS，ASA，HL等．
练习册系列答案
相关题目
