题目内容
直线y=kx+b,过点(1,-2)和(4,1).
(1)求这条直线的解析式;
(2)在平面直角坐标系中画出它的图象;
(3)这条直线与x轴相交于点A,与y轴相交于点B,坐标原点为点O,求△AOB的周长.
解:(1)∵点(1,-2)和(4,1)代入直线y=kx+b,
∴ ,解得
,解得 ,
,
∴直线的解析式为:y=x-3;
(2)∵直线的解析式为:y=x-3,
∴其图象如图所示:
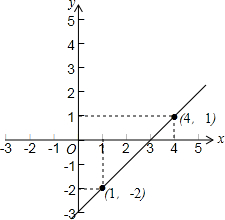
(3)∵直线的解析式为:y=x-3,与x轴相交于点A,与y轴相交于点B,
∴A(3,0),B(0,-3),
∴AB=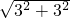 =3
=3 ,
,
∴△AOB的周长=3+3+3 =6+3
=6+3 .
.
分析:(1)把点(1,-2)和(4,1)代入直线y=kx+b求出k、b的值即可得出直线的解析式;
(2)在平面直角坐标系内描出点(1,-2)和(4,1),画出一次函数的图象即可;
(3)求出AB两点的坐标即可得出△AOB的周长.
点评:本题考查的是用待定系数法求一次函数的解析式及一次函数的性质,熟知用待定系数法求一次函数的解析式的基本步骤是解答此题的关键.
∴
 ,解得
,解得 ,
,∴直线的解析式为:y=x-3;
(2)∵直线的解析式为:y=x-3,
∴其图象如图所示:
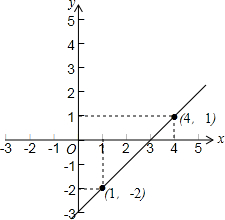
(3)∵直线的解析式为:y=x-3,与x轴相交于点A,与y轴相交于点B,
∴A(3,0),B(0,-3),
∴AB=
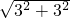 =3
=3 ,
,∴△AOB的周长=3+3+3
 =6+3
=6+3 .
.分析:(1)把点(1,-2)和(4,1)代入直线y=kx+b求出k、b的值即可得出直线的解析式;
(2)在平面直角坐标系内描出点(1,-2)和(4,1),画出一次函数的图象即可;
(3)求出AB两点的坐标即可得出△AOB的周长.
点评:本题考查的是用待定系数法求一次函数的解析式及一次函数的性质,熟知用待定系数法求一次函数的解析式的基本步骤是解答此题的关键.

练习册系列答案
相关题目
 (2013•海珠区一模)如图,直线y=kx-k+2与抛物线
(2013•海珠区一模)如图,直线y=kx-k+2与抛物线
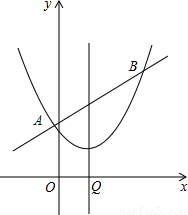 如图,直线y=kx-k+2与抛物线
如图,直线y=kx-k+2与抛物线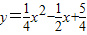 交于A、B两点,抛物线的对称轴与x轴交于点Q.
交于A、B两点,抛物线的对称轴与x轴交于点Q.