题目内容
已知二次函数y=a(a+1)x2-(2a+1)x+1.
(1)当此函数的图象与x轴有两个交点时,求a的取值范围;
(2)当a为正整数时,设此函数的图象与x轴相交于A、B两点,求线段AB的长;
(3)若a依次取1,2…,2010时,函数的图象与x轴相交所截得的2010条线段为A1B1,A2B2,…,A2010B2010,试求它们的长的和.
解:(1)依题意a的取值必须满足 ,
,
解得a为不等于0和-1的任意实数;
(2)设A、B两点坐标为A(x1,0)、B(x2,0),则x1,x2是方程a(a+1)x2-(2a+1)x+1=0的两个不等实根,
则AB的长为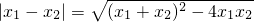 ①
①
∵ ,
,
代入①式得 ;
;
∵a为正整数,
∴ ;
;
(3)当a依次取1,2,…,2010时,所截得的线段长分别为 ,
, ,…
,…
, ,
,
∴|A1B1|+|A2B2|+…+|A2010B2010|,
=
 +…+
+…+ ,
,
= ,
,
=1- ,
,
= .
.
分析:(1)利用根的判别式与二次函数的定义解答即可;
(2)利用两点之间的距离公式以及根与系数的关系解答即可;
(3)顺次代入(2)中的通项,利用数的规律解决问题.
点评:此题考查二次函数图象与x轴交点坐标的特征、根与系数的关系、两点之间的距离公式以及运用数的规律灵活计算.
 ,
,解得a为不等于0和-1的任意实数;
(2)设A、B两点坐标为A(x1,0)、B(x2,0),则x1,x2是方程a(a+1)x2-(2a+1)x+1=0的两个不等实根,
则AB的长为
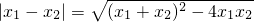 ①
①∵
 ,
,代入①式得
 ;
;∵a为正整数,
∴
 ;
;(3)当a依次取1,2,…,2010时,所截得的线段长分别为
 ,
, ,…
,…,
 ,
,∴|A1B1|+|A2B2|+…+|A2010B2010|,
=

 +…+
+…+ ,
,=
 ,
,=1-
 ,
,=
 .
.分析:(1)利用根的判别式与二次函数的定义解答即可;
(2)利用两点之间的距离公式以及根与系数的关系解答即可;
(3)顺次代入(2)中的通项,利用数的规律解决问题.
点评:此题考查二次函数图象与x轴交点坐标的特征、根与系数的关系、两点之间的距离公式以及运用数的规律灵活计算.

练习册系列答案
相关题目
已知二次函数y=-x2+bx+c的图象过点A(1,2),B(3,2),C(0,-1),D(2,3).点P(x1,y1),Q(x2,y2)也在该函数的图象上,当0<x1<1,2<x2<3时,y1与y2的大小关系正确的是( )
| A、y1≥y2 | B、y1>y2 | C、y1<y2 | D、y1≤y2 |
 (2013•莒南县二模)已知二次函数y=ax2+bx+c(a≠0)的图象如图所示,有下列5个结论:
(2013•莒南县二模)已知二次函数y=ax2+bx+c(a≠0)的图象如图所示,有下列5个结论: 已知二次函数y=ax2+bx+c(a≠0)的图象如图所示,则下列结论:①ac>0;②a-b+c<0;
已知二次函数y=ax2+bx+c(a≠0)的图象如图所示,则下列结论:①ac>0;②a-b+c<0;