Question

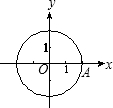如图，平面直角坐标系xOy中，点A（2，0），以OA为半径作⊙O，若点P，B都在⊙O上，且四边形AOPB为菱形，则点P的坐标为________．

Answer 1

，
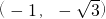
分析：根据菱形的性质可知△POB，△AOB是等边三角形，从而得出∠POM=180°-60°×2=60°，再根据三角函数即可求出OM，PM的长度，得到点P的坐标，注意点P可以在x轴的上方和下方．
解答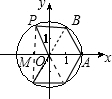：解：∵四边形AOPB为菱形
∴OP=PB=AB=OB，
∵OP=OB，
∴△POB，△AOB是等边三角形，
∴∠POM=180°-60°×2=60°，
∴OM=OP•cos∠POM=1，PM=OP•sin∠POM=．
当点P在x轴的上方时，P的坐标为（-1，）；
当点P在x轴的下方时，P的坐标为（-1，-）．
故答案为：（-1，），或（-1，-）．
点评：本题考查了菱形的性质，等边三角形的性质和三角函数，同时注意分类思想的运用．