题目内容
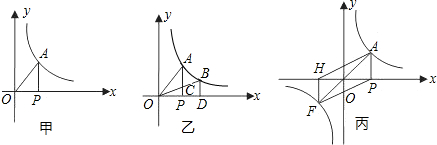
 有一个面积为1的正方形,经过一次“生长”后,在他的左右肩上生出两个小正方形,其中,三个正方形围成的三角形是直角三角形,再经过一次“生长”后,变成了右图,如果继续“生长”下去,它将变得“枝繁叶茂”,请你算出“生长”了2009次后形成的图形中所有的正方形的面积和是
有一个面积为1的正方形,经过一次“生长”后,在他的左右肩上生出两个小正方形,其中,三个正方形围成的三角形是直角三角形,再经过一次“生长”后,变成了右图,如果继续“生长”下去,它将变得“枝繁叶茂”,请你算出“生长”了2009次后形成的图形中所有的正方形的面积和是
- A.2008
- B.2009
- C.2010
- D.1
C
分析:根据勾股定理和正方形的面积公式,知“生长”1次后,以直角三角形两条直角边为边长的正方形的面积和等于以斜边为边长的正方形的面积,即所有正方形的面积和是2×1=2;“生长”2次后,所有的正方形的面积和是3×1=3,推而广之即可求解.
解答: 解:设直角三角形的是三条边分别是a,b,c.
解:设直角三角形的是三条边分别是a,b,c.
根据勾股定理,得
a2+b2=c2,
即正方形A的面积+正方形B的面积=正方形C的面积=1.
推而广之,“生长”了2009次后形成的图形中所有的正方形的面积和是2010×1=2010.
故选C.
点评:此题主要是能够根据勾股定理发现每一次得到的新的正方形的面积和与原正方形的面积之间的关系.
分析:根据勾股定理和正方形的面积公式,知“生长”1次后,以直角三角形两条直角边为边长的正方形的面积和等于以斜边为边长的正方形的面积,即所有正方形的面积和是2×1=2;“生长”2次后,所有的正方形的面积和是3×1=3,推而广之即可求解.
解答:
 解:设直角三角形的是三条边分别是a,b,c.
解:设直角三角形的是三条边分别是a,b,c.根据勾股定理,得
a2+b2=c2,
即正方形A的面积+正方形B的面积=正方形C的面积=1.
推而广之,“生长”了2009次后形成的图形中所有的正方形的面积和是2010×1=2010.
故选C.
点评:此题主要是能够根据勾股定理发现每一次得到的新的正方形的面积和与原正方形的面积之间的关系.

练习册系列答案
相关题目

 长度的速度沿y轴正方向运动,设D、E两点的运动时间为t秒.
长度的速度沿y轴正方向运动,设D、E两点的运动时间为t秒. 别交于点M、N,直线运动的时间为t(秒).
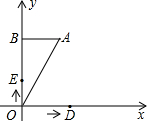
别交于点M、N,直线运动的时间为t(秒). (2010•本溪一模)在直角坐标系中,放置一个如图的直角三角形纸片AOB,已知OA=2,∠AOB=30°,D、E两点同时从原点O出发,D点以每秒
(2010•本溪一模)在直角坐标系中,放置一个如图的直角三角形纸片AOB,已知OA=2,∠AOB=30°,D、E两点同时从原点O出发,D点以每秒