题目内容
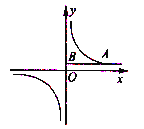
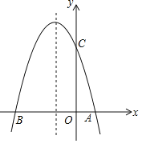
【题目】如图1,抛物线![]() 与
与![]() 轴交于
轴交于![]() 、
、![]() 两点,与
两点,与![]() 轴交于点
轴交于点![]() ,顶点为点
,顶点为点![]() .
.
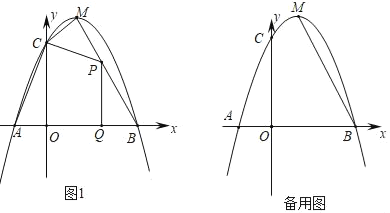
(1)求这条抛物线的解析式及直线![]() 的解析式;
的解析式;
(2)![]() 段
段![]() 上一动点(点
上一动点(点![]() 不与点
不与点![]() 、
、![]() 重合),过点
重合),过点![]() 向
向![]() 轴引垂线,垂足为
轴引垂线,垂足为![]() ,设
,设![]() 的长为
的长为![]() ,四边形
,四边形![]() 的面积为
的面积为![]() .求
.求![]() 与
与![]() 之间的函数关系式及自变量
之间的函数关系式及自变量![]() 的取值范围;
的取值范围;
(3)在线段![]() 上是否存在点
上是否存在点![]() ,使
,使![]() 为等腰三角形?若存在,请直接写出点
为等腰三角形?若存在,请直接写出点![]() 的坐标;若不存在,请说明理由.
的坐标;若不存在,请说明理由.
【答案】(1)![]() ,
,![]() ;(2)
;(2)![]()
![]() ,
,![]() 的取值范围是
的取值范围是![]() ;(3)
;(3)![]() 或
或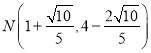 或
或![]()
【解析】
(1)将A、B俩点代入抛物线解析式即可求出M的坐标,再设直线![]() 的解析式为
的解析式为![]() , 代入M的值计算即可.
, 代入M的值计算即可.
(2)由已知![]() 轴,
轴,![]() ,可得点
,可得点![]() 的坐标为
的坐标为![]() ,再根据
,再根据![]() 即可求得t的值.
即可求得t的值.
(3)存在,根据等腰三角形的性质,分情况进行解答即可.
解:(1)∵抛物线![]() 与
与![]() 轴交于
轴交于![]() 、
、![]() 两点,
两点,
∴![]() ,
,
解得:![]() ,
,
∴二次函数的解析式为![]() ,
,
∵![]() ,
,
∴![]()
设直线的解析式为
![]() ,
,
则有
![]() ,
,
解得:![]() ,
,
∴直线![]() 的解析式为
的解析式为![]() ;
;
(2)∵![]() 轴,
轴,![]() ,
,
∴点![]() 的坐标为
的坐标为![]() ,
,
∴![]() ,
,
![]() ,
,
![]() ,
,
∵![]() 为线段
为线段![]() 上一动点(点
上一动点(点![]() 不与点
不与点![]() 、
、![]() 重合),
重合),
∴![]() 的取值范围是
的取值范围是![]() .
.
(3)线段![]() 上存在点
上存在点![]() ,
,![]() ,
,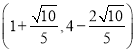 使
使![]() 为等腰三角形;
为等腰三角形;
![]() ,
,![]() ,
,![]() ,
,
①当![]() 时,
时,![]() ,
,
解得![]() ,
,![]() (舍去),
(舍去),
此时![]() ,
,
②当![]() 时,
时,![]() ,
,
解得![]() ,
,![]() (舍去),
(舍去),
此时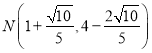 ,
,
③当![]() 时,
时,![]()
解得![]() ,此时
,此时![]() .
.

练习册系列答案
相关题目
【题目】某网店经市场调查,发现进价为40元的某新型文具每月的销售量y(件)与售价x(元)的相关信息如下:
售价x(元) | 60 | 70 | 80 | 90 | … |
销售量y(件) | 280 | 260 | 240 | 220 | … |
(1)试用你学过的函数来描述y与x的关系,这个函数可以是 (填“一次函数”、“反比例函数”或“二次函数”),并求这个函数关系式;
(2)当售价为多少元时,当月的销售利润最大,最大利润是多少;
(3)若获利不得高于进价的80%,那么售价定为多少元时,月销售利润达到最大,最大利润是多少?