Question

（本小题满分8分）如图，在平面直角坐标系中，点O是坐标原点，四边形AOCB是梯形，AB∥OC，点A在y轴上，点C在x轴上，且，OB＝OC．

   （1）求点B的坐标；

（2）点P从C点出发，沿线段CO以5个单位/秒的速度向终点O匀速运动，过点P作PH⊥OB，垂足为H，设△HBP的面积为S（S≠0），点P的运动时间为t秒，求S与t之间的函数关系式（直接写出自变量t的取值范围）；

（3）在（2）的条件下，过点P作PM∥CB交线段AB于点M，过点M作MR⊥OC，垂足为R，线段MR分别交直线PH、OB于点E、G，点F为线段PM的中点，联结EF．

①判断EF与PM的位置关系；

②当t为何值时，？

 

Answer 1

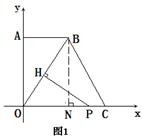
解：（1）如图1，过点B作BN⊥OC，垂足为N

∵，OB=OC

∴OA=8，OC=10      -------------------------------1分

∴OB=OC=10, BN=OA=8

∴ 

∴B (6,8)         ----------------------------------------------2分

（2）如图1，∵∠BON=∠POH,∠ONB=∠OHP=90°. 

∴△BON∽△POH    ∴

∵PC=5t.   ∴OP=10-5t.    ∴OH=6-3t. PH=8-4t.

  ∴BH=OB-OH=10-(6-3t)=3t+4   

∴ ------------------------------------ 3分

∴t的取值范围是：0≤t＜2      ------------------------------------------4分

 

（3）①EF⊥PM                         ----------------------------------------------------5分

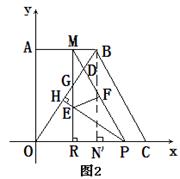∵MR⊥OC，PH⊥OB

∴∠RPM+∠RMP=90°，∠HPD+∠HDP=90° 

∵OC=OB     ∴∠OCB=∠OBC.

∵BC∥PM

∴∠RPM=∠HDP，∴∠RMP=∠HPD，即：∠ EMP=∠HPM

∴EM=EP

∵点F为PM的中点    ∴EF⊥PM      ----------6分

②如图2过点B作BN′⊥OC，垂足为 N′，BN′=8,CN′=4

∵BC∥PM,MR⊥OC

∴△MRP≌△B N′C

∴PR=C N′=4

设EM=x,则EP=x

在△PER中，∠ERP=90°，RE=MR-ME=8-x

有，∴x=5

∴ME=5

∵△MGB∽△N′BO     

∴

∵ PM∥CB，AB∥OC

∴四边形BMPC是平行四边形. ∴ BM=PC=5t.

 

第一种情况：当点G在点E上方时（如图2）

∵EG=2，∴MG=EM-EG=5-2=3

∴  ∴t=                                --------------------7分

 

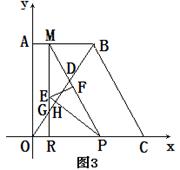
 第二种情况：当点G在点E下方时（如图3） MG=ME+EG=5+2=7，

∴ ，∴t=        -------------------------------------------8分

 ∴当t=或时，.      

 

 

 

解析:略