题目内容
如图,我校九年级某班数学课外活动小组利用周末开展课外实践活动,他们要在佳山公路上测量“佳山”高AB.于是他们采用了下面的方法:在佳山公路上选择了两个观察点C、D(C、D、B在一条直线上),从C处测得山顶A的仰角为30°,在D处测得山顶A的仰角为45°,已知测角仪的高CE与DF的高为1.5m,量得CD=450m.请你帮助他们计算出佳山高AB.(精确到1m, ,
, )
)
【答案】分析:连接EF并延长交AB于H,则可得到△AEH、△AFH均为直角三角形,在Rt△AFH中,根据∠AFH=45°得到AH=FH,最后设AH=FH=x (m),则EH=450+x 利用在Rt△AEH中,利用30°的正切值列出有关x的方程即可求解.
解答:解:连接EF并延长交AB于H,
则△AEH、△AFH均为直角三角形,
在Rt△AFH中,∵∠AFH=45°,
∴∠FAH=45°,∴AH=FH,
设AH=FH=x (m),则EH=450+x (m),
在Rt△AEH中,∵tan30°= ,
,
∴ ,
,
解得x=225 +225
+225
∴AB=225 +225+1.5≈225×1.73+226.5≈616(m).
+225+1.5≈225×1.73+226.5≈616(m).
答:佳山高约为616(m).
点评:本题要求学生借助仰角关系构造直角三角形,并结合图形利用三角函数解直角三角形.
解答:解:连接EF并延长交AB于H,
则△AEH、△AFH均为直角三角形,
在Rt△AFH中,∵∠AFH=45°,
∴∠FAH=45°,∴AH=FH,
设AH=FH=x (m),则EH=450+x (m),
在Rt△AEH中,∵tan30°=
 ,
,∴
 ,
,解得x=225
 +225
+225 ∴AB=225
 +225+1.5≈225×1.73+226.5≈616(m).
+225+1.5≈225×1.73+226.5≈616(m).答:佳山高约为616(m).
点评:本题要求学生借助仰角关系构造直角三角形,并结合图形利用三角函数解直角三角形.

练习册系列答案
相关题目
 AB.(精确到1m,
AB.(精确到1m, AB.(精确到1m,
AB.(精确到1m,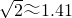 ,
,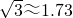 )
)