题目内容
如图△ABC中，AB=AC，BC=6，S△ABC=3，那么sinB=________．
分析：过A作AD⊥BC于D，求出BD=DC=3，根据三角形的面积求出AD，根据勾股定理求出AB，根据锐角三角函数的定义求出即可．
解答：
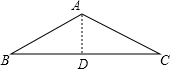解：过A作AD⊥BC于D，∵AB=AC，AD⊥BC，
∴BD=DC=3，
∵S△ABC=3，
∴
BC•AD=3，∴AD=1，
由勾股定理得：AB=
=
，∴sinB=
=
=
．故答案为：
．点评：本题主要考查对等腰三角形的性质，勾股定理，三角形的面积，锐角三角函数的定义等知识点的理解和掌握，构造直角三角形和求AD、AB的长是解此题的关键．
练习册系列答案
相关题目
13、如图△ABC中，AB=AC，BD平分∠ABC，且△ABC∽△BDC，则∠A=
8、如图△ABC中，AB=3，AC=2，BO平分∠ABC，CO平分∠ACB．DE过点O交AB于D，交AC于E，且DE∥BC．则△ADE周长为
如图△ABC中，AB=AC，M是BC中点，D，E分别在AB，AC上，且BD=CE，求证：ME=MD．
已知：如图△ABC中，AB=AC，AD和BE是高，它们交于点H，且AE=BE，
如图△ABC中，AB=6，AC=