题目内容
(12分)已知关于x的方程 .
.
(1)求证:无论m取任何实数时,方程恒有实数根;(3分)
(2)若关于x的二次函数 的图象与x轴两交点间的距离为2时,求抛物线的解析式。(4分)
的图象与x轴两交点间的距离为2时,求抛物线的解析式。(4分)
(3)在同一直角坐标系xOy中,画出(2)中所有函数图象,结合图象回答问题:当直线 与(2)中的这个函数图象只有两个交点时,求b的取值范围。(5分)
与(2)中的这个函数图象只有两个交点时,求b的取值范围。(5分)

(1)见解析;(2) ;(3)见解析
;(3)见解析
【解析】
试题分析:(1)方程分一元一次方程和一元二次方程两种情况讨论:当m=0时,为一元一次方程,方程有实根,当m≠0时,只要证明△≥0即可;(2)求出二次函数
 的图象与x轴两交点的坐标,根据两交点间的距离为2得以m为未知数的方程,解方程得m的值即可;(3)画出函数的图像,根据图像可得结论.
的图象与x轴两交点的坐标,根据两交点间的距离为2得以m为未知数的方程,解方程得m的值即可;(3)画出函数的图像,根据图像可得结论.
试题解析:
(1)当m=0时,为一元一次方程,方程有实根,
当m≠0时,因为△ ≥0,所以必有实根,综上所述,无论m为何值,方程恒有实根;
≥0,所以必有实根,综上所述,无论m为何值,方程恒有实根;
(2)令y=0时, ,解得
,解得 ,
, ,因为两交点间的距离为2,所以
,因为两交点间的距离为2,所以 ,解得
,解得 或
或 ,所以
,所以
(3)图像略:
根据图象可得:b> 或b<
或b< 或b=2时,y=x+b与(2)中函数只有两个公共点
或b=2时,y=x+b与(2)中函数只有两个公共点
考点:1.一元二次方程;2.求二次函数的解析式;3.二次函数图象的应用.

 新非凡教辅冲刺100分系列答案
新非凡教辅冲刺100分系列答案(本题8分) 求一个正数的算术平方根,有些数可以直接求得,如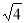 ,有些数则不能直接求得,如
,有些数则不能直接求得,如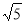 ,但可以通过计算器求. 还有一种方法可以通过一组数的内在联系,运用规律求得,请同学们观察下表:
,但可以通过计算器求. 还有一种方法可以通过一组数的内在联系,运用规律求得,请同学们观察下表:
n | 16 | 0.16 | 0.0016 | 1600 | 160000 | … |
| 4 | 0.4 | 0.04 | 40 | 400 | … |
(1)表中所给的信息中,你能发现什么规律?(请将规律用文字表达出来)
(2)运用你发现的规律,探究下列问题:已知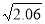
 1.435,求下列各数的算术平方根:
1.435,求下列各数的算术平方根:
①0.0206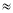 ; ②20600
; ②20600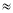 ;
;
(3)根据上述探究过程类比研究一个数的立方根已知
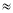 1.260,则
1.260,则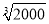
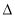 ABC中,∠C=90°,∠BAC=60°,AB=8.半径为
ABC中,∠C=90°,∠BAC=60°,AB=8.半径为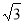 的⊙M与射线BA相切,切点为N,且AN=3.将Rt
的⊙M与射线BA相切,切点为N,且AN=3.将Rt 后得到Rt
后得到Rt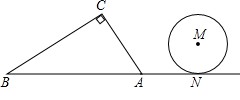
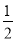 B.
B.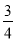 C.
C.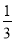 D.
D.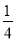
 的值为零,则x的值等于 .
的值为零,则x的值等于 .
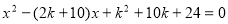 .
. 的部分图象如图所示,由图可知,关于x的方程
的部分图象如图所示,由图可知,关于x的方程 的
的

 的点相距3个单位长度的点所表示的数是 .
的点相距3个单位长度的点所表示的数是 .