题目内容
 已知AB是⊙O的直径,半径OC⊥AB,D为
已知AB是⊙O的直径,半径OC⊥AB,D为 上任意一点,E为弦BD上一点,且BE=AD,求证:△CDE为等腰直角三角形.
上任意一点,E为弦BD上一点,且BE=AD,求证:△CDE为等腰直角三角形.
 解:连接AC、BC,
解:连接AC、BC,由圆周角定理得∠CBE=∠CAD,
∵CO⊥AB,
∴点C是弧ABC的中点,
∴AC=BC,
又∵BE=AD
∴△ACD≌△BCE,
∴CD=CE.∠ADC=∠BEC,
∵AB是直径,
∴∠ADB=90°,
∵∠BEC=∠DCE+∠CDB,∠ADC=∠ADB+∠CDB,
∴∠DCE=∠ADB=90°,
即△DCE是等腰直角三角形.
分析:连接AC、BC,证△ACD≌△BCE和∠BCE=∠ADB=90°即可.
点评:本题利用了圆周角定理,全等三角形的判定和性质,直径对的圆周角是直角,三角形的外角等于与它不相邻的两个内角和,等腰直角三角形的判定求解.

练习册系列答案
 阳光课堂课时作业系列答案
阳光课堂课时作业系列答案
相关题目
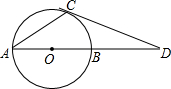 如图,已知AB是⊙O的直径,∠CAB=30°,过点C的⊙O的切线交AB延长线于D,若OD=
如图,已知AB是⊙O的直径,∠CAB=30°,过点C的⊙O的切线交AB延长线于D,若OD=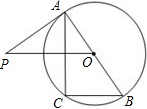 如图,已知AB是⊙O的直径,过点O作弦BC的平行线,交过点A的切线AP于点P,连接AC.
如图,已知AB是⊙O的直径,过点O作弦BC的平行线,交过点A的切线AP于点P,连接AC.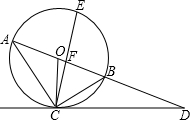

 如图,已知AB是⊙O的直径,AD切⊙O于点A,
如图,已知AB是⊙O的直径,AD切⊙O于点A,