题目内容
如图，P为矩形ABCD的边BC上的一个动点，对角线AC，BD相交于O点，且PE⊥BD于E，PF⊥AC于F，若AB=6，BC=8，则PE+PF的值为
- A.2.4
- B.4.8
- C.5
- D.10
B
分析：首先先设未知线段为未知数．再证得△BEP∽△BCD，从而可以求解．
解答：设PE为x，PF为a．BP为y，CP为b．
∵∠EBP=∠DBC，∠BEP=∠DCB．
∴△BEP∽△BCD．
∴
=
．
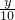同理证得
=
．
∴x+a=
（y+b）=4.8．
故选B．
点评：本题考查的是矩形的性质，应注意利用相似三角形得出比例进行求解．
分析：首先先设未知线段为未知数．再证得△BEP∽△BCD，从而可以求解．
解答：设PE为x，PF为a．BP为y，CP为b．
∵∠EBP=∠DBC，∠BEP=∠DCB．
∴△BEP∽△BCD．
∴
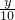=．同理证得
=．∴x+a=
（y+b）=4.8．故选B．
点评：本题考查的是矩形的性质，应注意利用相似三角形得出比例进行求解．
练习册系列答案
相关题目
26、如图，在等边△ABC中，点D是BC边的中点，以AD为边作等边△ADE．
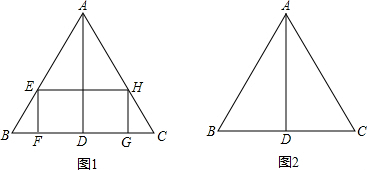
如图，四边形DEFG是△ABC的内接矩形，如果△ABC的高线AH长8cm，底边BC长10cm，设DG=xcm，DE=ycm，则y关于x的函数关系式为