题目内容
已知：如图，已知∠B=∠D=90°，∠A=60°，AB=10，CD=6．
求：四边形ABCD的面积．
解：
由题意得，AB=10，CD=6，∠A=60°，
在RT△ABE中，BE=ABtan∠A=10
，
在RT△DCE中，DE=CDcot∠E=6×=6．
故可得S四边形ABCD=S△ABE-S△DCE=
AB•BE-CD•DE=50-18=32．
即四边形ABCD的面积为32．
分析：延长AD、BC交于点E，根据∠A=60°，可分别求出BE，DE，从而利用S四边形ABCD=S△ABE-S△DCE，可得出答案．
点评：此题考查了勾股定理的知识，解答本题的技巧在于作出辅助线，利用面积差求出四边形ABCD的面积，难度一般．
由题意得，AB=10，CD=6，∠A=60°，
在RT△ABE中，BE=ABtan∠A=10
，在RT△DCE中，DE=CDcot∠E=6×
=6．故可得S四边形ABCD=S△ABE-S△DCE=
AB•BE-CD•DE=50-18=32．即四边形ABCD的面积为32
．分析：延长AD、BC交于点E，根据∠A=60°，可分别求出BE，DE，从而利用S四边形ABCD=S△ABE-S△DCE，可得出答案．
点评：此题考查了勾股定理的知识，解答本题的技巧在于作出辅助线，利用面积差求出四边形ABCD的面积，难度一般．
练习册系列答案
相关题目
19、如图，已知∠1=∠A，∠2=∠B，要证MN∥EF．请完善证明过程，并在括号内填上相应依据：
19、如图，已知AB是一条河，河的一边有两个村庄M和N，现要在河AB上修一个抽水站，请你在下图中作出抽水站的位置P，使点P到点M和点N的距离之和最短．
（2011•晋江市质检）如图，已知AB⊥CF，DE⊥CF，垂足分别为B、E，AB=DE．请添加一个适当条件，使△ABC≌△DEF，并予以证明．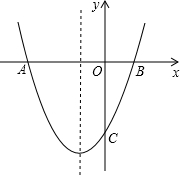
（2011•利川市一模）如图，已知：抛物线y=ax2+bx-4（a≠0）与x轴交于A、B两点，与y轴交于点C，A、B两点的坐标分别为A（-6，0）、B（2，0）．
如图，已知∠AGD=∠ACB，∠1=∠2．求证：CD∥EF．