Question

如图，平行四边形ABCD中，AB=2，BC=2，AC=4，过AC的中点O作EF⊥AC交AD于E，交BC于F，则EF=________．

Answer 1

分析：根据AB、BC、AC的长即可判定△ABC为直角三角形，根据EF⊥AC和∠ABC=90°可以判定△COF∽△CBA，即可求得=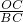，即可解题．
解答：∵∠ACB=∠DAC，AO=CO，∠COF=∠EOA，∴△CFO≌△AEO，∴OE=OF，
∵AB²+BC²=AC²，
∴∠ABC=90°，∴平行四边形ABCD为矩形，
矩形对角线互相平分，
∴OC=AC，
又∵EF⊥AC，∠ACB=∠FCO
∴△COF∽△CBA，∴=，
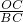∴OF=．
∴EF=2FO=，
故答案为．
点评：本题考查了相似三角形对应边比值相等的性质，考查了勾股定理的逆定理判定直角三角形的方法，考查了全等三角形的证明和全等三角形对应边相等的性质，本题中求证△COF∽△CBA是解题的关键．