题目内容
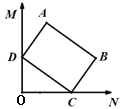
【题目】如图1,以矩形![]() 的顶点
的顶点![]() 为原点,
为原点,![]() 所在直线为
所在直线为![]() 轴,
轴,![]() 所在直线为
所在直线为![]() 轴,建立平面直角坐标系,顶点为点
轴,建立平面直角坐标系,顶点为点![]() 的抛物线
的抛物线![]() 经过点
经过点![]() ,点
,点![]() .
.
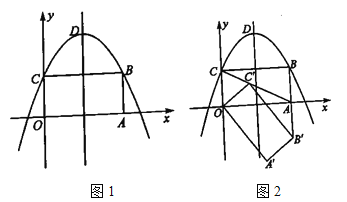
(1)写出抛物线的对称轴及点![]() 的坐标,
的坐标,
(2)将矩形![]() 绕点
绕点![]() 顺时针旋转
顺时针旋转![]() 得到矩形
得到矩形![]() .
.
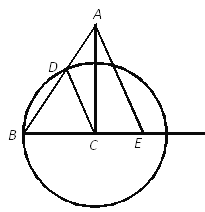
①当点![]() 恰好落在
恰好落在![]() 的延长线上时,如图2,求点
的延长线上时,如图2,求点![]() 的坐标.
的坐标.
②在旋转过程中,直线![]() 与直线
与直线![]() 分别与抛物线的对称轴相交于点
分别与抛物线的对称轴相交于点![]() ,点
,点![]() .若
.若![]() ,求点
,求点![]() 的坐标.
的坐标.
【答案】(1)对称轴:直线![]() ,
,![]() ;(2)①
;(2)①![]() ;②
;②![]() ,
,![]() .
.
【解析】
(1)首先根据矩形的性质以及A、C点的坐标确定点B的坐标,再利用待定系数法确定该抛物线的解析式.
(2) ①连结![]() 证明
证明![]() 即可解答
即可解答
②用全等或面积法证得![]() ,再分情况解得即可
,再分情况解得即可
解:(1)将y=0代入![]() 得C点的坐标为(0,1)则OC为1,则AB=1及B点的坐标为(2,1),再代入即可得对称轴:直线
得C点的坐标为(0,1)则OC为1,则AB=1及B点的坐标为(2,1),再代入即可得对称轴:直线![]()
(2)①连结![]() ,易知
,易知![]() ,
,
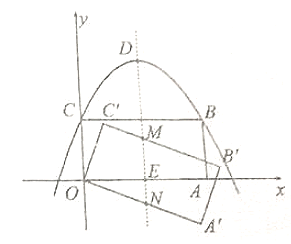
在![]() 和
和![]() 中,
中,
![]()
![]()
![]()
![]()
②可用全等或面积法证得![]() .(两张等宽纸条重叠部分为菱形)
.(两张等宽纸条重叠部分为菱形)
情况1:![]() ,如图.
,如图.
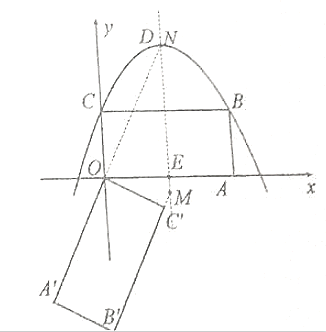
![]() 设
设![]() ,
,![]() ,
,
在![]() 中,
中,
![]()
![]() (舍去),
(舍去),![]()
![]()
情况2:![]() ,如图.
,如图. ![]()
此时点![]() 与点
与点![]() 重合,
重合,![]()
![]()
综上所述:![]() ,
,![]() .
.

练习册系列答案
相关题目