Question

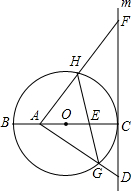（2012•高新区一模）如图，⊙O的直径BC=8，过点C作⊙O的切线m，D是直线m上一点，且DC=4，A是线段BO上一动点，连接AD交⊙O于点G，过点A作AF⊥AD交直线m于点F，交⊙O于点H，连接GH交BC于点E．
（1）当A是BO的中点时，求AF的长；
（2）若∠AGH=∠AFD，
①GE与EH相等吗？请说明理由；
②求△AGH的面积．

Answer 1

分析：（1）当点A是BO的中点时，根据△ACD∽△FCA，可将AF的长求出；
（2）①GE=EH，利用有两对角相等的两三角形相似可证明△AGH∽△AFD，根据相似三角形的性质得到：∠AGH=∠F=∠CAG，进而得到AE=GE=HE，所以GE=EH；
②（I）当GH为⊙O的直径时，根据△AGH∽△AFD，可将△AFD的面积求出；（II）当GH不是直径时，可知△AGH为等腰直角三角形，从而可将△AFD的面积求出．

解答：解：（1）∵BC=8，A是OB的中点，
∴AC=6，
又∵DC为⊙O的切线，
∴∠ACD=∠ACF=90°，
∵AD⊥AF，
∴∠ADC、∠CAF都和∠DAC互余，
∴∠ADC=∠CAF，
∴△ACD∽△FCA，
∴CD：AC=AC：FC
即4：6=6：FC，
∴FC=9，
∴AF=

AC2 +CF2

=

92+62

=3

13

；

（2）①GE=EH，
理由如下：
∵∠AGH=∠AFD，∠DAF=∠HAG，
∴△AGH∽△AFD，
∴∠AGH=∠F=∠CAG，∠AHG=∠D=∠CAF，
∴AE=GE=HE，
∴GE=EH，
②∵GE=EH，有垂径定理推论可知：GH是圆O的直径或GH是垂直于直径的弦，
如图1，（I）如果GH是直径（即A与B重合，E与O重合），那么GH=8；
在直角△AFD中，
∵∠ACD=∠ACF=90°，∠GAF=90°，
∴∠DAC+∠CAF=90°，∠F+∠CAF=90°，
∴∠F=∠DAC，
∴△DAC∽△AFC，
∴

AC

DC

=

CF

AC

，
∵AC=8，DC=4代入得：FC=16，
由勾股定理得：FD=20，
∵△AGH∽△AFD，
∴△AGH与△AFD相似比为2：5，
∴这两个相似三角形的面积比为4：25，
而△AFD的面积为=

1

2

×20×8=80，
∴△AGH的面积=

4

25

×80=

64

5

；
如图2，（II）如果GH不是直径，由GE=HE，
根据垂径定理的推论可得GH⊥BC，
∴AC垂直平分GH，
∴AG=AH，且GH∥FD，
而∠GAH=90°，则∠AGH=45°．
∴∠D=∠AGH=45°，
∴在直角三角形ACD中，∠DAC=45°．
∴AC=CD=4，
而OC=4，
∴A、O点重合，故AG=AH=4，
∴△AGH的面积=8．

点评：本题考查了相似三角形的判定以及性质、勾股定理的运用、垂径定理的运用，等腰直角三角形的性质综合应用，题目的综合性强，难度大，是一道不错的中考压轴题．