题目内容
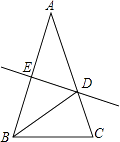
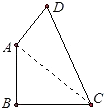
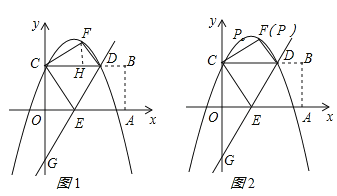
【题目】如图,在平面直角坐标系中,矩形OABC的顶点A,C分别在x轴和y轴的正半轴上,顶点B的坐标为(2m,m),翻折矩形OABC,使点A与点C重合,得到折痕DE,设点B的对应点为F,折痕DE所在直线与y轴相交于点G,经过点C,F,D的抛物线为![]() .
.
(1)求点D的坐标(用含m的式子表示);
(2)若点G的坐标为(0,﹣3),求该抛物线的解析式;
(3)在(2)的条件下,设线段CD的中点为M,在线段CD上方的抛物线上是否存在点P,使PM=![]() EA?若存在,直接写出点P的坐标;若不存在,说明理由.
EA?若存在,直接写出点P的坐标;若不存在,说明理由.

【答案】(1)D(![]() ,m);(2)
,m);(2)![]() ;(3)P(
;(3)P(![]() ,
,![]() )或(
)或(![]() ,
,![]() ).
).
【解析】
试题分析:(1)由折叠的性质得出CF=AB=m,DF=DB,∠DFC=∠DBA=90°,CE=AE,设CD=x,则DF=DB=2m﹣x,由勾股定理得出方程,解方程即可得出结果;
(2)由△OEG∽△CDG,即可求出m的值,从而得出C、D的坐标,作FH⊥CD于H,则△FCH∽△DCF,得出比例式求出F的坐标,用待定系数法即可求出抛物线的解析式;
(3)由直角三角形斜边上的中线性质得出MF=![]() CD=
CD=![]() EA,点P与点F重合,得出点P的坐标;由抛物线的对称性得另一点P的坐标即可.
EA,点P与点F重合,得出点P的坐标;由抛物线的对称性得另一点P的坐标即可.
试题解析:(1)根据折叠的性质得:CF=AB=m,DF=DB,∠DFC=∠DBA=90°,CE=AE,∠CED=∠AED,设CD=x,则DF=DB=2m﹣x,根据勾股定理得:![]() ,即
,即![]() ,解得:x=
,解得:x=![]() ,∴点D的坐标为:(
,∴点D的坐标为:(![]() ,m);
,m);
(2)∵四边形OABC是矩形,∴OA=2m,OA∥BC,∴∠CDE=∠AED,∴∠CDE=∠CED,∴CE=CD=![]() ,∴AE=CE=
,∴AE=CE=![]() ,∴OE=OA﹣AE=
,∴OE=OA﹣AE=![]() ,∵OA∥BC,∴△OEG∽△CDG,∴
,∵OA∥BC,∴△OEG∽△CDG,∴![]() ,即
,即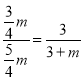 ,解得:m=2,∴C(0,2),D(
,解得:m=2,∴C(0,2),D(![]() ,2),作FH⊥CD于H,如图1所示:则∠FHC=90°=∠DFC,∵∠FCH=∠FCD,∴△FCH∽△DCF,∴
,2),作FH⊥CD于H,如图1所示:则∠FHC=90°=∠DFC,∵∠FCH=∠FCD,∴△FCH∽△DCF,∴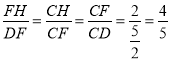 ,即
,即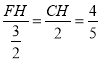 ,∴FH=
,∴FH=![]() ,CH=
,CH=![]() ,
,![]() =
=![]() ,∴F(
,∴F(![]() ,
,![]() ),把点C(0,2),D(
),把点C(0,2),D(![]() ,2),F(
,2),F(![]() ,
,![]() )代入
)代入![]() 得:
得: ,解得:
,解得:![]() ,
,![]() ,
,![]() ,∴抛物线的解析式为:
,∴抛物线的解析式为:![]() ;
;
(3)存在;理由如下:如图2所示:∵CD=CE,CE=EA,∴CD=EA,∵线段CD的中点为M,∠DFC=90°,∴MF=![]() CD=
CD=![]() EA,点P与点F重合,∴点P的坐标为:(
EA,点P与点F重合,∴点P的坐标为:(![]() ,
,![]() );
);
由抛物线的对称性得另一点P的坐标为(![]() ,
,![]() );
);
∴在线段CD上方的抛物线上存在点P,使PM=![]() EA,点P的坐标为:(
EA,点P的坐标为:(![]() ,
,![]() ),或(
),或(![]() ,
,![]() ).
).

 轻松暑假总复习系列答案
轻松暑假总复习系列答案