题目内容
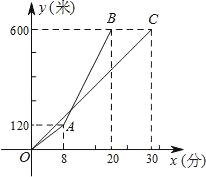
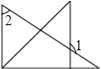
【题目】如图,在直角坐标系中,点A(-2,0),B(4,0),现同时将点A、B分别向上平移4个单位,再向右平移2个单位,得到点A、B的对应点C、D,连接AC,CD、BD.
(1)直接写出点C、D的坐标,求四边形ABDC的面积;
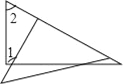
(2)动点P从点C出发,以每秒1个单位的速度,沿射线CO运动.设点P运动时间为t秒.连结PA,设三角形AOP的面积为S ,求S与t之间的关系式;
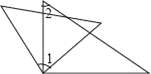
(3)如图,在(2)的条件下,在线段BO上取一点E,使2BE=OB,连接PB、CE相交于点F,当三角形AOP的面积是四边形ABDC的![]() 时,求点F的坐标.
时,求点F的坐标.

【答案】(1)(1)C(0,4)D(6,4)![]() =24;(2)见解析;(3)F(
=24;(2)见解析;(3)F(![]() ,
,![]() )
)
【解析】
(1)根据向右平移横坐标加,向上平移纵坐标加写出点C、D的坐标即可,再根据平行四边形的面积公式列式计算即可得解;
(2)分点P在点O上方时求出OP的长度,然后再表示三角形AOP的面积;点P在点O下方时,求出OP的长,然后再表示三角形AOP的面积;
(3)求出点P、E的坐标,然后利用待定系数法求出直线CE、BP的解析式,联立求出点F的坐标即可得解.
解:(1)∵点A(-2,0),B(4,0)分别向上平移4个单位,再向右平移2个单位,
∴点C、D的坐标分别为(0,4),(6,4),
S四边形ABDC=6×4=24;
(2)①点P在点O上方时,OP=4-t,OA=2,
∴S=4-t,
②点P在点O下方时,OP=t-4,OA=2,
∴S=t-4;
(3)当三角形AOP的面积是四边形ABDC的![]() 时,
时,
4-t=![]() ×24 ,
×24 ,
解得t=1,
∴P(0,3),
∵2BE=OB,
∴E(2,0),
易求直线CE的解析式为y=-2x+4,
直线BG的解析式为y=-![]() x+3,
x+3,
联立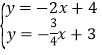 ,
,
解得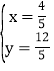 ,
,
∴点F 的坐标为(![]() ,
,![]() ).
).

练习册系列答案
 教学练新同步练习系列答案
教学练新同步练习系列答案
相关题目