Question

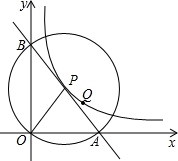
如图，直线y=kx-2分别交x轴、y轴于点A、B，点P为AB上一点且PC为△AOB的中位线，PC的延长线交反比例函数y=

3

x

的图象于点Q，若PQ=

5

2

，求k的值．

Answer 1

∵一次函数y=kx-2的图象交y轴于点B，
∴令x=0，得到y=-2，
∴B（0，-2），即OB=2，
又PC为△AOB的中位线，
∴PC=

1

2

OB=1，PC∥OB．
∵OB⊥OA，∴PQ⊥OA，
∵PQ=

5

2

，
∴CQ=

5

2

-1=

3

2

，
∴点Q的纵坐标为

3

2

，
将y=

3

2

代入y=

3

x

中得：

3

2

=

3

x

，解得：x=2，
∴Q（2，

3

2

），
∴OC=2，
∴P（2，-1），
把P（2，-1）代入y=kx-2得：2k-2=-1，
则k=

1

2

．