题目内容
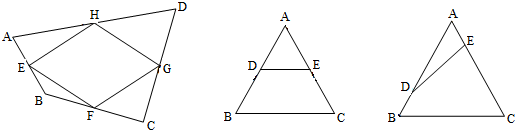
顺次连接四边形ABCD各边的中点E、F、G、H，所得到的四边形EFGH的面积与四边形ABCD的面积的比为
- A.
- B.
- C.
- D.
B
分析：根据中位线的性质可得到△BEF∽△BAC，由相似三角形的面积比是相似比的平方求得S△BEF=S△BAC．同理知S△AHE=S△ADB，S△DGH=S△DCA，S△CFG=S△CBD．最后，利用分割法求四边形EFGH的面积与四边形ABCD的面积的比．
解答：
解：如图，连接AC、BD．
在△ABC中，点E、F分别是边AB、BC的中点，
∴EF是△ABC的中位线，
∴EF=AC，△BEF∽△BAC，
∴
=
=，
∴S△BEF=S△BAC．
同理，S△AHE=S△ADB，S△DGH=S△DCA，S△CFG=S△CBD．
则S四边形EFGH=S四边形ABCD-S△BAC-S△AHE-S△DGH-S△CFG=S四边形ABCD，即S四边形EFGH：S四边形ABCD=1：2；
故选B．
点评：此题主要利用正方形的周长公式和面积公式进行计算，中位线性质是本题的关键．
分析：根据中位线的性质可得到△BEF∽△BAC，由相似三角形的面积比是相似比的平方求得S△BEF=
S△BAC．同理知S△AHE=S△ADB，S△DGH=S△DCA，S△CFG=S△CBD．最后，利用分割法求四边形EFGH的面积与四边形ABCD的面积的比．解答：
解：如图，连接AC、BD．在△ABC中，点E、F分别是边AB、BC的中点，
∴EF是△ABC的中位线，
∴EF=
AC，△BEF∽△BAC，∴
==，∴S△BEF=
S△BAC．同理，S△AHE=
S△ADB，S△DGH=S△DCA，S△CFG=S△CBD．则S四边形EFGH=S四边形ABCD-S△BAC-S△AHE-S△DGH-S△CFG=
S四边形ABCD，即S四边形EFGH：S四边形ABCD=1：2；故选B．
点评：此题主要利用正方形的周长公式和面积公式进行计算，中位线性质是本题的关键．
练习册系列答案
导学教程高中新课标系列答案
相关题目
如图，若已知△ABC中，D、E分别为AB、AC的中点，则可得DE∥BC，且DE=
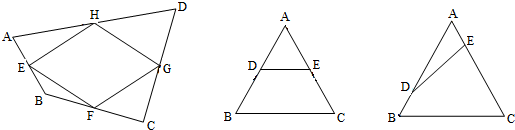
如图，在边长为1的正方形网格中，△A′B′C′与△ABC是中心对称图形．
