题目内容
【题目】如图甲,![]() ,
,![]() ,
,![]() ,垂足分别为
,垂足分别为![]() ,且三个垂足在同一直线上.
,且三个垂足在同一直线上.
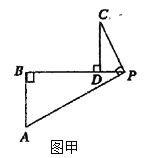
(1)证明:![]() ;
;
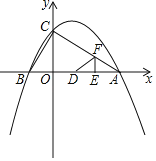
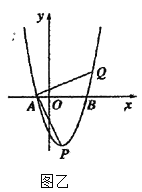
(2)已知地物线![]() 与
与![]() 轴交于点
轴交于点![]() ,顶点为
,顶点为![]() ,如图乙所示,若
,如图乙所示,若![]() 是抛物线上异于
是抛物线上异于![]() 的点,使得
的点,使得![]() ,求
,求![]() 点坐标(提示:可结合第(1)小题的思路解答)
点坐标(提示:可结合第(1)小题的思路解答)
【答案】(1)证明见解析;(2)![]()
【解析】
(1)根据同角的余角相等求出∠A=∠CPD,然后求出△ABP和△PCD相似,再根据相似三角形对应边成比例列式整理即可得证;
(2)根据抛物线解析式求出点P的坐标以及点A和点B的坐标,再过点P作PC⊥x轴于C,设AQ与y轴相交于D,然后求出PC、AC的长,再根据(1)的结论求出OD的长,从而得到点D的坐标,利用待定系数法求出直线AD的解析式,与抛物线解析式联立求解即可得到点Q的坐标.
(1)证明:![]() ,
,![]() ,
,![]() ,
,
![]() ,
,
![]()
![]() ,
,
![]() ,
,
![]() ,
,
![]() ,
,
![]() ;
;
(2)过![]() 作
作![]() ,
,![]() ,
,
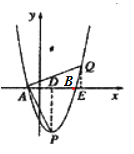
设![]() ,则E(x,0),
,则E(x,0),
∴AE=x+1,QE=x2-2x-3,.
令![]() ,则
,则![]() ,
,
解得![]() ,
,![]() ,
,
![]()
![]() ,
,
又![]()
![]() ,
,
![]() ,
,
∴D(1,0),
∴AD=2,PD=4.
由(1)得![]() ,
,
即![]() ,
,
解得![]() ,
,![]() (舍去),
(舍去),
当![]() 时,
时,![]() ,
,
![]() .
.

练习册系列答案
 全能测控期末小状元系列答案
全能测控期末小状元系列答案
相关题目