题目内容
如图，ABCD是长方形，以BC为直径的半圆与AD边只有一个交点，且AB=x，则阴影部分的面积为
- A.
- B.
- C.
- D.
A
分析：设半圆与AD的交点是E，连接OE，BE，通过△EDB的面积等于△BOE的面积可知阴影部分的面积等于扇形OBE的面积，求扇形OBE的面积即可．
解答：
解：设半圆与AD的交点是E，连接OE，BE
∵△EDB的面积等于△BOE的面积（等底等高）
∴阴影部分的面积等于扇形OBE的面积
∵OB=AB=x，∠BOE=90°
即S阴影=
故选A．
点评：主要考查了通过割补法把不规则图形转化为规则图形求面积的方法．本题的关键是利用等底等高的方法确定△EDB的面积等于△BOE的面积从而得到阴影部分的面积等于扇形OBE的面积．
分析：设半圆与AD的交点是E，连接OE，BE，通过△EDB的面积等于△BOE的面积可知阴影部分的面积等于扇形OBE的面积，求扇形OBE的面积即可．
解答：
解：设半圆与AD的交点是E，连接OE，BE∵△EDB的面积等于△BOE的面积（等底等高）
∴阴影部分的面积等于扇形OBE的面积
∵OB=AB=x，∠BOE=90°
即S阴影=
故选A．
点评：主要考查了通过割补法把不规则图形转化为规则图形求面积的方法．本题的关键是利用等底等高的方法确定△EDB的面积等于△BOE的面积从而得到阴影部分的面积等于扇形OBE的面积．
练习册系列答案
相关题目
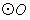的半径为2，点A、B、C在
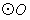上，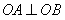
，
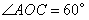，P是OB上一动点，求PA+PC的最小值；
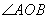内一点，PO=8，Q，R分别是OA、OB上的动点，求
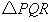周长的最小值． 
