题目内容
在Rt△ABC中,斜边c=10,两直角边a≤8,b≥8,则a+b的最大值是
- A.
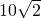
- B.14
- C.

- D.16
B
分析:已知一斜边的长,分别假设两直角为8,然后根据勾股定理求得另一直角边的长,再结合题意进行分析从而求解.
解答:∵在Rt△ABC中,斜边c=10,两直角边a≤8,b≥8.
∴①当a=8时,b=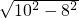 =6<8,不符合题意,故舍去;
=6<8,不符合题意,故舍去;
②当b=8时,a=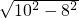 =6<8,符合题意;
=6<8,符合题意;
∴a+b的最大值=6+8=14.
故选B.
点评:此题主要考查学生对勾股定理的理解及运用,注意由勾股定理求的值要代入条件看是否符合题意.
分析:已知一斜边的长,分别假设两直角为8,然后根据勾股定理求得另一直角边的长,再结合题意进行分析从而求解.
解答:∵在Rt△ABC中,斜边c=10,两直角边a≤8,b≥8.
∴①当a=8时,b=
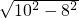 =6<8,不符合题意,故舍去;
=6<8,不符合题意,故舍去;②当b=8时,a=
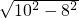 =6<8,符合题意;
=6<8,符合题意;∴a+b的最大值=6+8=14.
故选B.
点评:此题主要考查学生对勾股定理的理解及运用,注意由勾股定理求的值要代入条件看是否符合题意.

练习册系列答案
相关题目
 的位置,其中
的位置,其中 分别是A、B对应点,且点B在斜边
分别是A、B对应点,且点B在斜边 交AB于D,这时∠BDC的度数是
交AB于D,这时∠BDC的度数是

 的位置,其中
的位置,其中 分别是A、B对应点,且点B在斜边
分别是A、B对应点,且点B在斜边 交AB于D,这时∠BDC的度数是
交AB于D,这时∠BDC的度数是