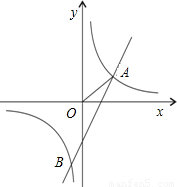
题目内容
 两个反比例函数
两个反比例函数 和
和 在第一象限内的图象如图所示,点P在
在第一象限内的图象如图所示,点P在 的图象上,PC⊥x轴于点C,交
的图象上,PC⊥x轴于点C,交 的图象于点A,PD⊥y轴于点D,交
的图象于点A,PD⊥y轴于点D,交 的图象于点B,当点P在
的图象于点B,当点P在 的图象上运动时,以下结论不正确的是
的图象上运动时,以下结论不正确的是
- A.△ODB与△OCA的面积相等
- B.四边形PAOB的面积不会发生变化
- C.PA与PB始终相等
- D.当点A是PC的中点时,点B一定是PD的中点
C
分析:A、D、由于A、B两点在 上,根据反比例函数的对称性(对称轴为y=x),易知A、D正确;
上,根据反比例函数的对称性(对称轴为y=x),易知A、D正确;
B、由于A、B在y= 上,根据反比例函数的性质可以得到S△OAC=S△OBD=
上,根据反比例函数的性质可以得到S△OAC=S△OBD= ,SPCOD=k,由此可推出四边形PAOB的面积不会发生变化;
,SPCOD=k,由此可推出四边形PAOB的面积不会发生变化;
C、当且仅当PCOD为正方形时PA=PB.
解答:根据反比例函数的对称性(对称轴为y=x),易知A、D正确;
∵A、B在y= 上,
上,
∴xy=1,
∴S△OAC=S△OBD= ,
,
∴SPCOD=k,
∴四边形PAOB的面积不会发生变化,为k-1,
∴B正确;
D中当且仅当PCOD为正方形时PA=PB.
故选C.
点评:此题主要利用了反比例函数具有轴对称性(对称轴是y=x或y=-x)和中心对称性(关于原点对称).
分析:A、D、由于A、B两点在
 上,根据反比例函数的对称性(对称轴为y=x),易知A、D正确;
上,根据反比例函数的对称性(对称轴为y=x),易知A、D正确;B、由于A、B在y=
 上,根据反比例函数的性质可以得到S△OAC=S△OBD=
上,根据反比例函数的性质可以得到S△OAC=S△OBD= ,SPCOD=k,由此可推出四边形PAOB的面积不会发生变化;
,SPCOD=k,由此可推出四边形PAOB的面积不会发生变化;C、当且仅当PCOD为正方形时PA=PB.
解答:根据反比例函数的对称性(对称轴为y=x),易知A、D正确;
∵A、B在y=
 上,
上,∴xy=1,
∴S△OAC=S△OBD=
 ,
,∴SPCOD=k,
∴四边形PAOB的面积不会发生变化,为k-1,
∴B正确;
D中当且仅当PCOD为正方形时PA=PB.
故选C.
点评:此题主要利用了反比例函数具有轴对称性(对称轴是y=x或y=-x)和中心对称性(关于原点对称).

练习册系列答案
相关题目
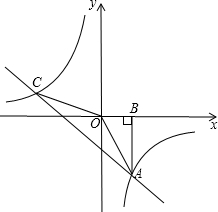 如图,Rt△AOB的顶点A是一次函数y=-x+(k+1)的图象与反比例函数y=
如图,Rt△AOB的顶点A是一次函数y=-x+(k+1)的图象与反比例函数y=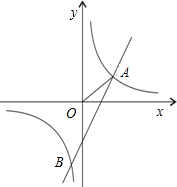 如图,已知反比例函数
如图,已知反比例函数 和一次函数y=2x-b图象都经过点A(1,1)
和一次函数y=2x-b图象都经过点A(1,1)