题目内容
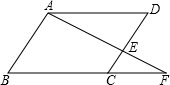已知平行四边形ABCD，F是BC的延长线上一点，连接AF交CD于E点．EF=3，AE=4，CE=2，求AB的长．
解：∵EF=3，AE=4
∴AF=EF+AE=7．
∵平行四边形ABCD中CE∥AB．
∴△ABF∽△ECF
∴
=
即：
=
．解得AB=
．
分析：ABCD是平行四边形，则CE∥AB，得到△ABF∽△ECF，根据相似三角形对应边的比相等即可求解．
点评：本题主要考查了平行于三角形一边的直线与另两边相交，形成的三角形与原三角形相似；以及相似三角形的性质，相似三角形的对应边的比相等．
∴AF=EF+AE=7．
∵平行四边形ABCD中CE∥AB．
∴△ABF∽△ECF
∴
=即：
=．解得AB=．分析：ABCD是平行四边形，则CE∥AB，得到△ABF∽△ECF，根据相似三角形对应边的比相等即可求解．
点评：本题主要考查了平行于三角形一边的直线与另两边相交，形成的三角形与原三角形相似；以及相似三角形的性质，相似三角形的对应边的比相等．
练习册系列答案
浙大优学小学年级衔接捷径浙江大学出版社系列答案
相关题目
20、如图，已知平行四边形ABCD．
，连接DF，并延长DF交AB的延长线于点E，连接CE．
49、如图，已知平行四边形ABCD，AE平分∠DAB交DC于E，BF平分∠ABC交DC于F，DC=6cm，AD=2cm，求DE、EF、FC的长．
已知平行四边形ABCD中，对角线BD平分∠ABC，求证：四边形ABCD是菱形．