题目内容
某超市一月份的营业额为20万元，一月、二月、三月的营业额共100万元．如果平均每月的增长率为x，则根据题意列出的方程应为（ ）
| A、20（1+x）2=100 |
| B、20+20×2x=100 |
| C、20+20×3x=100 |
| D、20[1+（1+x）+（1+x）2]=100 |
考点：由实际问题抽象出一元二次方程
专题：增长率问题
分析：可先表示出二月份的营业额，那么二月份的营业额×（1+增长率）=三月份的营业额，等量关系为：一月份的营业额+二月份的营业额+三月份的营业额=100，把相应数值代入即可求解．
解答：解：二月份的营业额为20×（1+x），三月份的营业额在二月份营业额的基础上增加x，
为20×（1+x）×（1+x），则列出的方程是20+20（1+x）+20（1+x）2=100，
故选D．
为20×（1+x）×（1+x），则列出的方程是20+20（1+x）+20（1+x）2=100，
故选D．
点评：考查求平均变化率的方法．若设变化前的量为a，变化后的量为b，平均变化率为x，则经过两次变化后的数量关系为a（1±x）2=b；注意本题的等量关系为3个月的营业额之和．
练习册系列答案
相关题目
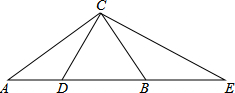如图，在Rt△ABC中，∠ACB=90°，AC=b，AB=c．若D、E分别是AB和AB延长线上的两点，BD=BC，CE⊥CD，则以AD和AE的长为根的一元二次方程是（ ）| A、x2-2cx+b2=0 |
| B、x2-cx+b2=0 |
| C、x2-2cx+b=0 |
| D、x2-cx+b=0 |
已知0和-1都是某个方程的解，此方程是（ ）
| A、x2-1=0 |
| B、x（x+1）=0 |
| C、x2-x=0 |
| D、x2=x+1 |
两个数的商是正数，那么这两个数（ ）
| A、和为正 | B、差为正 |
| C、积为正 | D、以上都不是 |
已知：如图，在△ABC中，D是边BC上一点，BE⊥AD，CF⊥AD，垂足分别为E、F．