题目内容
(1999•昆明)已知:二次函数y= 的图象与x轴从左到右的两个交点依次为A、B,与y轴交点为C;
的图象与x轴从左到右的两个交点依次为A、B,与y轴交点为C;(1)求A、B、C三点的坐标;
(2)求过B、C两点的一次函数的解析式;
(3)如果P(x,y)是线段BC上的动点,O为坐标原点,试求△POA的面积S与x之间的函数关系式,并求出自变量x的取值范围;
(4)是否存在这样的点P,使得PO=AO?若存在,求出点P的坐标;若不存在说明理由.
【答案】分析:(1)抛物线的解析式中,令x=0可求得C点坐标,令y=0可求得A、B的坐标;
(2)已知了B、C的坐标,用待定系数法求解即可;
(3)根据直线BC的解析式可用x表示出P点的纵坐标,以OA为底,P点纵坐标的绝对值为高即可得到△OAP的面积,由此可求得S、x的函数关系式;
(4)易知△OBC是等腰Rt△,且直角边长为6,因此点O到BC的距离为3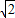 (即
(即 ),显然这个距离要大于4,因此P点的坐标无论去何值,都不存在OP=OA的情况.
),显然这个距离要大于4,因此P点的坐标无论去何值,都不存在OP=OA的情况.
解答: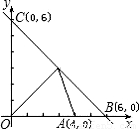 解:(1)由题意,在y=
解:(1)由题意,在y= x2-
x2- 中,令x=0及y=0
中,令x=0及y=0
可得:A(4,0),B(6,0),C(0,6);(3分)
(2)设一次函数的解析式为:y=kx+b;(4分)
将B(6,0)、C(0,6)代入上式,得:
 ,
,
解得 ;
;
∴y=-x+6;(5分)
(3)根据题意得S△POA= ×4×y,
×4×y,
∴y=-x+6;
∴S△POA=-2x+12;(7分)
∴0≤x<6;(8分)
(4)∵|OB|=|OC|,∠COB=90°;
∴△BOC是等腰直角三角形;
当OP⊥BC时,OP最短;
OP= BC=
BC=
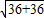 =3
=3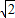 =
=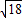 ,(10分)
,(10分)
而OA=4,
∴ >4;(11分)
>4;(11分)
∴不存在这样的点P,使得OP=AO.(12分)
点评:此题考查了二次函数与坐标轴交点坐标的求法、一次函数解析式的确定、图形面积的计算方法等重要知识点,综合性较强,难度适中.
(2)已知了B、C的坐标,用待定系数法求解即可;
(3)根据直线BC的解析式可用x表示出P点的纵坐标,以OA为底,P点纵坐标的绝对值为高即可得到△OAP的面积,由此可求得S、x的函数关系式;
(4)易知△OBC是等腰Rt△,且直角边长为6,因此点O到BC的距离为3
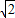 (即
(即 ),显然这个距离要大于4,因此P点的坐标无论去何值,都不存在OP=OA的情况.
),显然这个距离要大于4,因此P点的坐标无论去何值,都不存在OP=OA的情况.解答:
 解:(1)由题意,在y=
解:(1)由题意,在y= x2-
x2- 中,令x=0及y=0
中,令x=0及y=0可得:A(4,0),B(6,0),C(0,6);(3分)
(2)设一次函数的解析式为:y=kx+b;(4分)
将B(6,0)、C(0,6)代入上式,得:
 ,
,解得
 ;
;∴y=-x+6;(5分)
(3)根据题意得S△POA=
 ×4×y,
×4×y,∴y=-x+6;
∴S△POA=-2x+12;(7分)
∴0≤x<6;(8分)
(4)∵|OB|=|OC|,∠COB=90°;
∴△BOC是等腰直角三角形;
当OP⊥BC时,OP最短;
OP=
 BC=
BC=
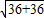 =3
=3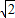 =
=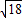 ,(10分)
,(10分)而OA=4,
∴
 >4;(11分)
>4;(11分)∴不存在这样的点P,使得OP=AO.(12分)
点评:此题考查了二次函数与坐标轴交点坐标的求法、一次函数解析式的确定、图形面积的计算方法等重要知识点,综合性较强,难度适中.

练习册系列答案
相关题目
 的图象与x轴从左到右的两个交点依次为A、B,与y轴交点为C;
的图象与x轴从左到右的两个交点依次为A、B,与y轴交点为C; = .
= .

