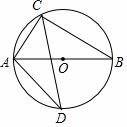
题目内容
如图所示,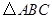 是
是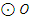 的内接三角形,
的内接三角形, ,
,
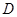 为
为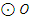 中弧AB上一点,延长
中弧AB上一点,延长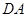 至点
至点 ,使
,使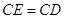 .
.
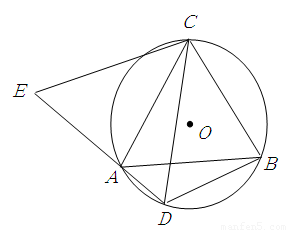
(1)求证: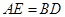 ;
;
(2)若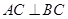 ,求证:
,求证: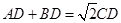 .
.
【答案】
(1)详见解析;(2)详见解析.
【解析】
试题分析:(1)由题意知,⊿ABC和⊿ECD都是等腰三角形,根据“同弧所对的圆周角相等”可知,∠ABC=∠ADC,由此可得,∠ACE=∠BCD,结合已知条件,利用“SAS”可证⊿ACE≌⊿BCD,所以有AE=BD.(2)若AC⊥BC,则有(1)的结论可知,∠DCE=90°,DE=AD+BD,又已知CD=CE,所以三角形DCE是等腰直角三角形,DE= CD,所以得证.规律:在解决圆中的线段相等关系或角相等时,常常要借助于三角形全等.
CD,所以得证.规律:在解决圆中的线段相等关系或角相等时,常常要借助于三角形全等.

试题解析:证明:(1)由同弧所对的圆周角相等,知∠ ∠
∠ .
.
∵ ,
, ,∴
∠
,∴
∠ ∠
∠ ∠
∠ ∠
∠ ,
,
∴ ∠ ∠
∠ ,
,
∴∠DCE-∠ACD=∠ACB-∠ACD
即:∠ ∠
∠ .
.
又∵ ,
, ,
,
∴ △ ≌△
≌△ . ∴
. ∴
 5分
5分
(2) ∵  ,∴
,∴ 
∵  ,∴
∠
,∴
∠ , ∴
∠
, ∴
∠ ∠
∠ .
.
由勾股定理,得
又∵ , ∴
, ∴
 ,∴
,∴  ,
,
∴  .
10分
.
10分
考点:1、全等三角形的判定和性质;2、圆周角定理.

练习册系列答案
相关题目
 10、如图所示.△ABC内接于⊙O,若∠OAB=28°,则∠C的大小是( )
10、如图所示.△ABC内接于⊙O,若∠OAB=28°,则∠C的大小是( ) (1)解方程:
(1)解方程: