题目内容
【题目】如图,已知二次函数![]() 的图象经过点
的图象经过点![]() ,与
,与![]() 轴分别交于点
轴分别交于点![]() ,点
,点![]() .点
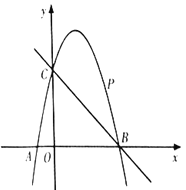
.点![]() 是直线
是直线![]() 上方的抛物线上一动点.
上方的抛物线上一动点.
(1)求二次函数![]() 的表达式;
的表达式;
(2)连接![]() ,
,![]() ,并把
,并把![]() 沿
沿![]() 轴翻折,得到四边形
轴翻折,得到四边形![]() .若四边形
.若四边形![]() 为菱形,请求出此时点
为菱形,请求出此时点![]() 的坐标;
的坐标;
(3)当点![]() 运动到什么位置时,四边形
运动到什么位置时,四边形![]() 的面积最大?求出此时
的面积最大?求出此时![]() 点的坐标和四边形
点的坐标和四边形![]() 的最大面积.
的最大面积.
【答案】(1)该二次函数的表达式为![]() ;(2)点P的坐标为(
;(2)点P的坐标为(![]() ,
,![]() );(3)P点的坐标为
);(3)P点的坐标为![]() ,四边形ABPC的面积的最大值为
,四边形ABPC的面积的最大值为![]() .
.
【解析】(1)根据待定系数法,可得函数解析式;
(2)根据菱形的对角线互相平分,可得P点的纵坐标,根据函数值与自变量的对应关系,可得答案;
(3)根据面积的和差,可得二次函数,根据二次函数的性质,可得m的值,根据自变量与函数值的对应关系,可得P点坐标.
【解答】(1)将点B和点C的坐标代入![]() ,
,
得 ![]() ,解得
,解得![]() ,
,![]() .
.
∴ 该二次函数的表达式为![]() .
.
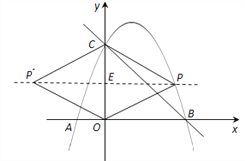
(2)若四边形POP′C是菱形,则点P在线段CO的垂直平分线上;
如图,连接PP′,则PE⊥CO,垂足为E,
∵ C(0,3),
∴ E(0,![]() ),
),
∴ 点P的纵坐标等于![]() .
.
∴ ![]() ,
,
解得![]() ,
,![]() (不合题意,舍去),
(不合题意,舍去),
∴ 点P的坐标为(![]() ,
,![]() ).
).
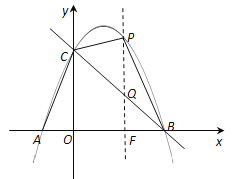
(3)过点P作y轴的平行线与BC交于点Q,与OB交于点F,
设P(m,![]() ),设直线BC的表达式为
),设直线BC的表达式为![]() ,
,
则 ![]() , 解得
, 解得 ![]() .
.
∴直线BC的表达式为 ![]() .
.
∴Q点的坐标为(m,![]() ),
),
∴![]() .
.
当![]() ,
,
解得![]() ,
,
∴ AO=1,AB=4,
∴ S四边形ABPC =S△ABC+S△CPQ+S△BPQ
=![]()
=![]()
=![]() .
.
当![]() 时,四边形ABPC的面积最大.
时,四边形ABPC的面积最大.
此时P点的坐标为![]() ,四边形ABPC的面积的最大值为
,四边形ABPC的面积的最大值为![]() .
.

练习册系列答案
 时刻准备着暑假作业原子能出版社系列答案
时刻准备着暑假作业原子能出版社系列答案 暑假衔接教材期末暑假预习武汉出版社系列答案
暑假衔接教材期末暑假预习武汉出版社系列答案 假期作业暑假成长乐园新疆青少年出版社系列答案
假期作业暑假成长乐园新疆青少年出版社系列答案
相关题目