题目内容
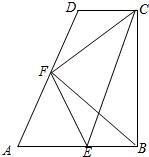 24、在直角梯形ABCD中,AB∥DC,AB⊥BC,∠A=60°,AB=2CD,E、F分别为AB、AD的中点,连接EF、EC、BF、CF;
24、在直角梯形ABCD中,AB∥DC,AB⊥BC,∠A=60°,AB=2CD,E、F分别为AB、AD的中点,连接EF、EC、BF、CF;(1)判断四边形AECD的形状;(不需要说理)
(2)△CDF与△BEF全等吗?请说明理由.
分析:(1)根据已知条件,结合图形,得出AE∥CD且AE⊥CD,根据性质一组对边平行且相等的四边形为平行四边形,可知四边形AECD是平行四边形.
(2)根据三角形全等的判定条件,结合题意和图形可以找到相关的线段和角度的关系,利用“SAS”得到△CDF≌△BEF.
(2)根据三角形全等的判定条件,结合题意和图形可以找到相关的线段和角度的关系,利用“SAS”得到△CDF≌△BEF.
解答:解:(1)平行四边形.
理由:∵AB=2CD,E为AB的中点,
∴AE=CD,
∵AB∥DC
∴四边形AECD为平行四边形.
(2)
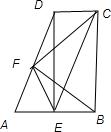 连接DE,得四边形BCDE是矩形,所以∠AED=90°,
连接DE,得四边形BCDE是矩形,所以∠AED=90°,
又∵F是AD的中点,
∴EF=DF=AF,
因为∠A=60°,
得△AEF是等边三角形,
从而∠BEF=∠CDF=120°,
∵CD=BE,
根据“SAS”得到△CDF≌△BEF.
理由:∵AB=2CD,E为AB的中点,
∴AE=CD,
∵AB∥DC
∴四边形AECD为平行四边形.
(2)
 连接DE,得四边形BCDE是矩形,所以∠AED=90°,
连接DE,得四边形BCDE是矩形,所以∠AED=90°,又∵F是AD的中点,
∴EF=DF=AF,
因为∠A=60°,
得△AEF是等边三角形,
从而∠BEF=∠CDF=120°,
∵CD=BE,
根据“SAS”得到△CDF≌△BEF.
点评:本题综合了直角梯形、平行四边形、全等三角形的性质以及判定,是一道综合性比较强的试题,解决综合性的题目就要求有很好的功底,可以清楚明白的看懂每一个知识点,平时应该熟练掌握小知识点.

练习册系列答案
 孟建平小学滚动测试系列答案
孟建平小学滚动测试系列答案 黄冈天天练口算题卡系列答案
黄冈天天练口算题卡系列答案
相关题目
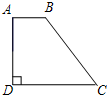 如图,在直角梯形ABCD中,AB∥DC,∠D=90°,若AD=8,BC=10,则cosC的值为( )
如图,在直角梯形ABCD中,AB∥DC,∠D=90°,若AD=8,BC=10,则cosC的值为( )A、
| ||
B、
| ||
C、
| ||
D、
|
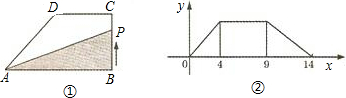
 如图,在直角梯形ABCD中,AD∥BC,AB⊥BC,且AB=BC=4AD,E是AB上的一点,DE⊥EC.求证:CE平分∠BCD.
如图,在直角梯形ABCD中,AD∥BC,AB⊥BC,且AB=BC=4AD,E是AB上的一点,DE⊥EC.求证:CE平分∠BCD. 如图,在直角梯形ABCD中,∠A=∠B=90°,∠C=45°,AB=4,AD=5,把梯形沿过点D的直线折叠,使点A刚好落在BC边上,则此时折痕的长为
如图,在直角梯形ABCD中,∠A=∠B=90°,∠C=45°,AB=4,AD=5,把梯形沿过点D的直线折叠,使点A刚好落在BC边上,则此时折痕的长为 如图,在直角梯形ABCD中,若AD=5,点A的坐标为(-2,7),则点D的坐标为( )
如图,在直角梯形ABCD中,若AD=5,点A的坐标为(-2,7),则点D的坐标为( )