题目内容
二次函数y=2x2+mx-5的图象与x轴交于点A（x1，0）、B（x2，0），且x12+x22=
，则m的值为（ ）
| 29 |
| 4 |
| A、3 | B、-3 |
| C、3或-3 | D、以上都不对 |
考点：抛物线与x轴的交点
专题：
分析：利用已知将原式变形得出x12+x22=（x1+x2）2-2x1x2，进而利用根与系数关系求出即可．
解答：解：∵二次函数y=2x2+mx-5的图象与x轴交于点A（x1，0）、B（x2，0），且x12+x22=
，
∴x12+x22=（x1+x2）2-2x1x2=
-2×（-
）=
，
解得：m=±3，
故选：C．
| 29 |
| 4 |
∴x12+x22=（x1+x2）2-2x1x2=
| m2 |
| 4 |
| 5 |
| 2 |
| 29 |
| 4 |
解得：m=±3，
故选：C．
点评：此题主要考查了根与系数的关系，得出x12+x22=（x1+x2）2-2x1x2是解题关键．
练习册系列答案
相关题目
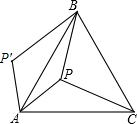如图，P是正三角形ABC内的一点，且PA=5，PB=12，PC=13，若将△PAC绕点A逆时针旋转后，得到△P′AB，求点P与点P′之间的距离及∠APB的度数．
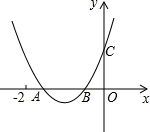如图，二次函数y=ax2+bx+c的图象与x轴交于A、B两点，与y轴交于点C，且OB=OC，下列结论：①b＞1且b≠2；②b2-4ac＜4a2；③a＞