Question

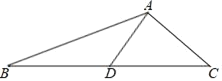
【题目】如图，在△ABC中，AD是BC边上的中线，AB＝5，AC＝3，AD＝2，

求：（1）BC的长；

（2）△ABC的面积．

Answer 1

【答案】（1）BC＝2；（2）6.

【解析】

（1）延长AD至E，使DE＝AD，连接BE，证明△ADC≌△EDB，再根据勾股定理即可求出；（2）把三角形ABC的面积转换成三角形ABE的面积即可求出.

解：（1）延长AD至E，使DE＝AD，连接BE，

∵AD为BC边上的中线，

∴BD＝DC，

在△ADC与△EDB中

，

∴△ADC≌△EDB（SAS），

∴BE＝AC＝3，

在△ABE中，AB＝5，BE＝3，AE＝2+2＝4，

即52＝32+42，即AB2＝BE2+AE2，

∴△ABE是直角三角形，

∴BD＝，

∴BC＝2BD＝2，

（2）∵△ABE是直角三角形，

∴S△ABE＝，

∵△ADC≌△EDB，

∴S△EDB＝S△ADC，

∴S△ABC＝S△ABE＝6