题目内容
19、已知?ABCD,分别以BC,CD为边向外等边△BCE和△DCF,则△AEF是( )

分析:在平行四边形ABCD中,由△BCE和△DCF是等边三角形,利用边角关系可得△ABE≌△FDA,即AE=AF,同理可得EF=AF,进而可得出△AEF的形状.
解答:解:在平行四边形ABCD中,
∵△BCE和△DCF是等边三角形,
则AB=DF,BE=AD,∠ABE=∠ABC+60°,∠ADF=∠ADC+60°,
∵∠ABC=∠ADC,
∴∠ABE=∠ADF,
∴△ABE≌△FDA,
即AE=AF,
同理AB=CF,CE=BE,∠ECF=∠ABE=∠ABC+60°,
∴△ABE≌△CFE,
∴AE=EF,进而可得AF=EF
即AE=EF=AF
∴△AEF是等边三角形.
故选B.
∵△BCE和△DCF是等边三角形,
则AB=DF,BE=AD,∠ABE=∠ABC+60°,∠ADF=∠ADC+60°,
∵∠ABC=∠ADC,
∴∠ABE=∠ADF,
∴△ABE≌△FDA,
即AE=AF,
同理AB=CF,CE=BE,∠ECF=∠ABE=∠ABC+60°,
∴△ABE≌△CFE,
∴AE=EF,进而可得AF=EF
即AE=EF=AF
∴△AEF是等边三角形.
故选B.
点评:本题主要考查了平行四边形的性质,等边三角形的性质及全等三角形的判定及性质问题,应熟练掌握平行四边形及等边三角形的性质,并能熟练运用.

练习册系列答案
相关题目
 10、如图,已知E,F分别为平行四边形ABCD边AD,AB上的两点,则图形中与△BEC的面积相等的三角形有( )
10、如图,已知E,F分别为平行四边形ABCD边AD,AB上的两点,则图形中与△BEC的面积相等的三角形有( )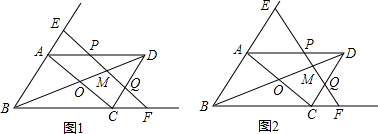
 已知?ABCD,分别以BC,CD为边向外作等边△BCE和△DCF,则△AEF是
已知?ABCD,分别以BC,CD为边向外作等边△BCE和△DCF,则△AEF是 ABCD,分别延长BC,DA至点E,F,如果∠E=∠F。
ABCD,分别延长BC,DA至点E,F,如果∠E=∠F。